Алгебра: Розв язати нерівність означає?

Розв'язати нерівність означає?

Показать ответ

Ответ:

помогиииитееее2233

08.07.2021 00:07

Ну насчет столбиком шутки шутками, а ведь можно делить многочлен на многочлен уголком, только в LaTeX это особо не распишешь. А вот разложить на множители вполне можно.

Сначала займемся числителем:

$y^5-2y^3+y^2+y-1=y^5-y^4+y^4-y^3-y^3+y^2+y-1=\\ =y^4(y-1)+y^3(y-1)-y^2(y-1)+1\cdot(y-1)=\\ =(y-1)(y^4+y^3-y^2+1)=(y-1)(y^4+y^3-y^2+y-y+1)=\\ (y-1)(y^3(y+1)-y(y+1)+1\cdot(y+1))=(y-1)(y+1)(y^3-y+1)$

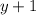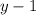Здесь часто использовался метод искусственного добавления и вычитания слагаемых для вынесения за скобки общих множителей (в виде скобок). Вот каких - дело опыта, но имея опыт с нахождением корней многочленов высоких степеней, я уже знал, конечно, что в разложении будут присутствовать скобки y+1 и y-1 и последнюю скобку не стал раскладывать, тоже кое-что зная. Так что больше опыта нужно и внимательности. Других рекомендаций нет.

Получили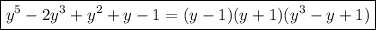 $\boxed{y^5-2y^3+y^2+y-1=(y-1)(y+1)(y^3-y+1)}$

Теперь знаменатель: по известной формуле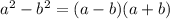 a^2-b^2=(a-b)(a+b)

получаем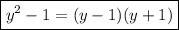 $\boxed{y^2-1=(y-1)(y+1)}$

Осталось все это написать вместе и сократить

$$\frac{(y-1)(y+1)(y^3-y+1)}{(y-1)(y+1)} =y^3-y+1; y\neq \pm1$

Сокращать можно только учитывая ограничения

ответ: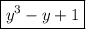 $\boxed{y^3-y+1}$

0,0(0 оценок)

Ответ:

Дора18119

03.03.2022 04:30

Квадратный трёхчлен разложен на множители: х^2+6х-27=(х+9)(х-а)
Найдите а
* * * Значение а можно разделить разными

x²+6x -27 = x²+2x*3+3² -3² -27 = (x+3)² - 36 = (x+3)² - 6² =  (x+3 + 6)(x+3 -6) =
(x+9)(x -3) ответ : a =3
* * *  x² +6x -27 =(x -x₁)(x -x₂) , где x₁ и x₂ корни квадратного трёхчлена
(можно было найти решая уравнение  x² +6x -27 = 0 ) * * *

x²+6x-27=(x+9)(x-а) ⇒ x - a = (x²+6x-27) : (x+9) разделить столбиком или
найти по схеме Горнера

(x+9)(x-а) = x² +9x -ax -9a = x² +(9 -a)x -9a
x²+6x - 27 ≡ x² +(9 -a)x - 9a   ⇔  { -27 = - 9a ;  6 = 9 -a .

0,0(0 оценок)

Популярные вопросы: Алгебра