Перепишем уравнение эллипса, поменяв местами параметры и :
При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.
Найдём эксцентриситет:
Найдём фокальное расстояние (полурасстояние между фокусами):
Тогда расстояние между фокусами в два раза больше: .
ответ: 6 ед.
На чертеже изображён данный эллипс. и — его фокусы.
Объяснение:
1) cos²x + 0,1cosx = 0
нужно для удобства вынести cos²x за скобки:
cos²x( 1 + 0,1) = 0
1,1 * cos²x = 0
мы можем просто поделить левую и правую часть на одно и тоже число, например на 1,1 , дабы избавиться от этого бесполезного числа :)
1,1 / 1,1 это 1 ; а 0 / 1,1 это 0:
cos²x = 0 /// с квадратом также
и получаем:
cos x = 0
косинус x равен нулю только в точке:
x= π/2 + πn , где n€ Z
2) sin тут не совсем понятно, объясните в комментариях к этой записи, что именно тут написано sin x или вы хотели sin²x?
Каноническое уравнение, задающее эллипс, выглядит так:
Перепишем уравнение эллипса, поменяв местами параметры
и 
:
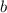При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.
Найдём эксцентриситет:
Найдём фокальное расстояние (полурасстояние между фокусами):
Тогда расстояние между фокусами в два раза больше: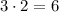
.
ответ: 6 ед.
На чертеже изображён данный эллипс.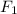
и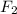 
— его фокусы.