Подобные одночлены - это одночлены, которые состоят из одних и тех же букв, в одинаковых степенях, но с разными или одинаковыми коэффициентами (числовыми множителями).
В этих выражениях требуется представить одинаковые множители как степень одного множителя.
1. -3,1*babab = -3,1*, подобным ему будет 2/5
2. 2 1/3*ba*(-3) = -7, подобным ему будет -3,1
3. 1/5bab*2 = 2/5a, подобным ему будет -7a
Похоже это задание на внимательность, чтобы правильно понимать смысл подобных одночленов и не вестись на одинаковые коэффициенты.
Пусть sinx - cosx = t,
преобразуем для sin2x
(sinx - cosx)^2 = t^2
1 - sin2x = t^2
sin2x = 1 - t^2
Следовательно, у нас выходит новое квадратное уравнение относительно замены
Отрешаем его:
- 5(1 - t^2) - 16t + 8 = 0
- 5 + 5t^2 - 16t + 8 = 0
5t^2 - 16t + 3 = 0
(5t - 1)*( t - 3) = 0
t = 1/5
t = 3
Выполним обратную замену
1)
sinx - cosx = 3
нет решений (пустое множ-во)
2)
sinx - cosx = 1/5
Возведём обе части уравнения в квадрат
1 - 2sinxcosx=1/25
sin2x = 24/25
sin2x = 0,96
2x = arcsin 0,96 + 2pik
x = 1/2*arcsin 0,96 + pik
2x = pi - arcsin 0,96 + 2pik
x = 1/2*(pi - arcsin 0,96) + pik
ОТВЕТ:
x = 1/2*arcsin 0,96 + pik, k ∈ Z
x = 1/2*(pi - arcsin 0,96) + pik, k ∈ Z
Подобные одночлены - это одночлены, которые состоят из одних и тех же букв, в одинаковых степенях, но с разными или одинаковыми коэффициентами (числовыми множителями).
В этих выражениях требуется представить одинаковые множители как степень одного множителя.
1. -3,1*babab = -3,1*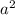
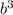, подобным ему будет 2/5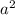
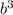
2. 2 1/3*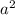
ba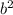
*(-3) = -7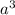
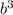, подобным ему будет -3,1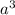
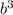
3. 1/5bab*2 = 2/5a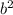
, подобным ему будет -7a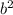
Похоже это задание на внимательность, чтобы правильно понимать смысл подобных одночленов и не вестись на одинаковые коэффициенты.