1) 11
2) 4
Объяснение:
1) 20 + 8х - х² > 0
- х²+8x+20 = 0
D = 64+80 = 144 =
x1 = x2 =
- -2 + 10 -
Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î
Нам подходит промежуток (-2; 10)
Определим целые числа в промежутке: -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Всего целых решений: 11
2) 4x² - 17x + 4 ≤ 0
4x² - 17x + 4 = 0
D = 289-64 = 225 =
+ - 4 +
Нам подходит промежуток [; 4]
Определим целые числа в промежутке: 1, 2, 3, 4
Всего целых решений: 4
1) 11
2) 4
Объяснение:
1) 20 + 8х - х² > 0
- х²+8x+20 = 0
D = 64+80 = 144 =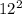
x1 =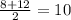 x2 =
x2 = 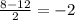
- -2 + 10 -
Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î
Нам подходит промежуток (-2; 10)
Определим целые числа в промежутке: -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Всего целых решений: 11
2) 4x² - 17x + 4 ≤ 0
4x² - 17x + 4 = 0
D = 289-64 = 225 =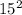
x1 =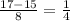 x2 =
x2 = 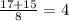
+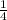 - 4 +
- 4 +
Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î
Нам подходит промежуток [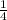 ; 4]
; 4]
Определим целые числа в промежутке: 1, 2, 3, 4
Всего целых решений: 4
2) приравниваем её к нулю и решаем получившееся уравнение
3) Смотрим: какие корни попали в указанный промежуток и ищем значения данной функции в этих точках и на концах данного отрезка;
4) пишем ответ.
Поехали?
1) f'(x) = ((x² -8x)'(x+1) - (x² -8x)(x+1)')/(x+1)²=
((2x-8)(x+1) - (x²-8x))/(x+1)²= (2x² -8x +2x -8 - x² +8x)/(x+1)²=
=(x² +2x -8) / (х+1)²
2)(x² +2x -8) / (х+1)² ⇒ x² +2x -8 =0, ⇒ х = - 4 и х = 2
3) Из найденных корней в указанный промежуток попало х = -4
а) х = -4
f(-4) = (-4)² -8*(-4) /(-4+1) = 48/(-2) = -24
б) х = -5
f(-5) = (-5)² -8*(-5) /(-5+1) = 65/(-4) = -13,75
в) х = -2
f(-2) = (-2)² -8*(-2)/(-2+1) = 20/(-1) = -20
4) maxf(x) = f((-2) = -20
minf(x) = f(-4) = -24