Для начала представим все многочлены в виде произведений простых чисел.
А так и останется.
Заметим, что у всех трёх произведений одинаковые основания у множетелей: 3 и 7. Это даёт нам возможность сравнивать показатели степеней множителей.
Сравним и . Показатели степени 7 у обоих произведений одинаковы, а вот степень тройки справа на один больше, чем слева. Поэтому правое выражение больше левого.
Сравним и . Показатели степени 3 у обоих произведений одинаковы, а вот степень семёрки справа на один больше, чем слева. Поэтому правое выражение больше левого.
Объяснение:
Для начала представим все многочлены в виде произведений простых чисел.
А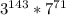
так и останется.
Заметим, что у всех трёх произведений одинаковые основания у множетелей: 3 и 7. Это даёт нам возможность сравнивать показатели степеней множителей.
Сравним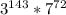
и 
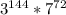. Показатели степени 7 у обоих произведений одинаковы, а вот степень тройки справа на один больше, чем слева. Поэтому правое выражение больше левого.
Сравним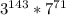
и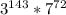 
. Показатели степени 3 у обоих произведений одинаковы, а вот степень семёрки справа на один больше, чем слева. Поэтому правое выражение больше левого.
Получаем следующий порядок:
х+z/2=1
x-z=3
выражаем х через z,получилось:
3+z+0,5z=1 (1) (1)3+z+0,5z=1
x=3+z 3+1,5z=1
1,5z=-2
z=-2/1,5
z=-1,3
получили систему
x=3-1,3
z=-1,3
ответ:х=1,7 и z=-1,3.
Но лучше спроси у одноклассников.