В базисе векторы имеют следующие координаты:
Их координаты попарно не пропорциональны, поэтому эти векторы не коллинеарны между собой.
Докажем компланарность векторов двумя
школьный (≈10 класс)
Признак компланарности трёх векторов:
Пусть векторы и не коллинеарны. Если для вектора существует единственная пара реальных чисел A и B, такая, что , то векторы компланарны.
Покажем, что
Слева и справа стоят координаты векторов. Векторы равны, если равны их соответственные координаты:
Сложим первое и второе уравнение, получим:
-1 = B
Подставим значение B в первое уравнение, найдём A:
3 = -A - (-1)
A = -2
Проверим найденные значения для остальных уравнений системы.
Итого получаем:
То есть признак выполнен. Значит векторы компланарны.
обычно проходится в вузах):
Векторы компланарны, если
Проверим это условие для данных векторов:
Следовательно, векторы компланарны.
Объяснение:
x²-19x+g=0 , x1=x , x2=x1+3
(podstawlajem)
{x1² - 19x1+g=0
{(x1+3)²-19*(x1+3)+g=0
{x1²-19x1+g=0
{x1²+6x1+9-19x1-57+g=0
{x1²-13x1-48+g=0
{x1²-13x1+g=48 * (-1)
{ x1²-19x1+g=0
(+) {-x1²+13x1-g=-48 (składywajem)
-6x1=-48
x1=8
(podstawlajem x1=8 do (1) urawnienija x²-19x+g=0
8²-19*8+g=0
64-152+g=0
g=88
kwdratowe urawnienije ma postać: x²-19x+88=0
po formule VIETA liczymy wtoroj korień x2
x1*x2=g
8*x2=88 // : 8
x2=11
В базисе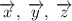 векторы имеют следующие координаты:
векторы имеют следующие координаты:
Их координаты попарно не пропорциональны, поэтому эти векторы не коллинеарны между собой.
Докажем компланарность векторов двумя
школьный (≈10 класс)
Признак компланарности трёх векторов:
Пусть векторы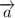 и
и 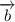 не коллинеарны. Если для вектора
не коллинеарны. Если для вектора 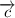 существует единственная пара реальных чисел A и B, такая, что
существует единственная пара реальных чисел A и B, такая, что  , то векторы
, то векторы 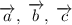 компланарны.
компланарны.
Покажем, что
Слева и справа стоят координаты векторов. Векторы равны, если равны их соответственные координаты:
Сложим первое и второе уравнение, получим:
-1 = B
Подставим значение B в первое уравнение, найдём A:
3 = -A - (-1)
A = -2
Проверим найденные значения для остальных уравнений системы.
Итого получаем:
То есть признак выполнен. Значит векторы компланарны.
обычно проходится в вузах):
Векторы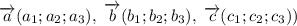 компланарны, если
компланарны, если
Проверим это условие для данных векторов:
Следовательно, векторы компланарны.
Объяснение:
x²-19x+g=0 , x1=x , x2=x1+3
(podstawlajem)
{x1² - 19x1+g=0
{(x1+3)²-19*(x1+3)+g=0
{x1²-19x1+g=0
{x1²+6x1+9-19x1-57+g=0
{x1²-19x1+g=0
{x1²-13x1-48+g=0
{x1²-19x1+g=0
{x1²-13x1+g=48 * (-1)
{ x1²-19x1+g=0
(+) {-x1²+13x1-g=-48 (składywajem)
-6x1=-48
x1=8
(podstawlajem x1=8 do (1) urawnienija x²-19x+g=0
8²-19*8+g=0
64-152+g=0
g=88
kwdratowe urawnienije ma postać: x²-19x+88=0
po formule VIETA liczymy wtoroj korień x2
x1*x2=g
8*x2=88 // : 8
x2=11