В решении.
Объяснение:
Установіть відповідність між формулами лінійних функцій (1 – 4) та
розташуванням їхніх графіків (А – Д).
1. у = х + 5 А. у ІІІ та ІV чвертях
2. у = -2х Б. у І, ІІ та ІІІ чвертях
3. у = - 5 В. у ІІ та ІV чвертях
4. у = 2 Г. у І та ІІІ чвертях
Д. у І та ІІ чвертях
ответы:
1. у = х + 5 Б. у І, ІІ та ІІІ чвертях
2. у = -2х В. у ІІ та ІV чвертях
3. у = - 5 А. у ІІІ та ІV чвертях
4. у = 2 Д. у І та ІІ чвертях
1) Log 8 (10 - x) = Log 8 7
10 - x = 7
x = 3
2) f(x)=y=2x^3-5x^2+1
F(x) = (2x^4)/4 - (5x^3)/3 + x + C
3) - 4 (sina)^2 + 5 - 4(cosa)^2
-4(sin^2 a + cos^2 a) + 5
-4 + 5 = 1
4) (1/3)^x-1 (1/9)
(1/3)^x-1 (1/3)^2
x-1 2
x 3
1) Показатели логарифмов одни и те же, значит можно отбросить весь логарифм и решать только его значения
2) Функция F(x) является первообразной функции f(x)
Все первообразные функции f(x) имеют вид: F(x) + C
3) Если вынести 4 из синуса и косинуса, то в скобках получится основное тригонометрическое тождество, которое равно 1
4) Приводим неравенство к одному основание, затем по правилу меняем знак неравенства, так как основание меньше 1
В решении.
Объяснение:
Установіть відповідність між формулами лінійних функцій (1 – 4) та
розташуванням їхніх графіків (А – Д).
1. у = х + 5 А. у ІІІ та ІV чвертях
2. у = -2х Б. у І, ІІ та ІІІ чвертях
3. у = - 5 В. у ІІ та ІV чвертях
4. у = 2 Г. у І та ІІІ чвертях
Д. у І та ІІ чвертях
ответы:
1. у = х + 5 Б. у І, ІІ та ІІІ чвертях
2. у = -2х В. у ІІ та ІV чвертях
3. у = - 5 А. у ІІІ та ІV чвертях
4. у = 2 Д. у І та ІІ чвертях
1) Log 8 (10 - x) = Log 8 7
10 - x = 7
x = 3
2) f(x)=y=2x^3-5x^2+1
F(x) = (2x^4)/4 - (5x^3)/3 + x + C
3) - 4 (sina)^2 + 5 - 4(cosa)^2
-4(sin^2 a + cos^2 a) + 5
-4 + 5 = 1
4) (1/3)^x-1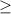 (1/9)
(1/9)
(1/3)^x-1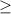 (1/3)^2
(1/3)^2
x-1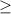 2
2
x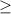 3
3
Объяснение:
1) Показатели логарифмов одни и те же, значит можно отбросить весь логарифм и решать только его значения
2) Функция F(x) является первообразной функции f(x)
Все первообразные функции f(x) имеют вид: F(x) + C
3) Если вынести 4 из синуса и косинуса, то в скобках получится основное тригонометрическое тождество, которое равно 1
4) Приводим неравенство к одному основание, затем по правилу меняем знак неравенства, так как основание меньше 1