Алгебра: с этим во очень поставлю 5 звёзд !

с этим во очень поставлю 5 звёзд !

Показать ответ

Ответ:

colaboyy7704ox6ktx

01.02.2023 08:53

№1

а) 3х²=12х

3х²-12х=0

х(3х-12)=0

х₁=0; х₂=4.

ответ: х₁=0; х₂=4.

б) х⁴-2х²=8

(х²)²-2х²-8=0

Пусть х²=t, тогда

t²-2t-8=0

D=(-2)²-4*1*(-8)=36

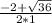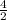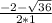t₁= $\frac{-2+\sqrt{36} }{2*1}$ = $\frac{4}{2}$ = 2

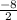t₂= $\frac{-2-\sqrt{36} }{2*1}$ = $\frac{-8}{2}$ = -4

Вернёмся к уравнению:

1) х²=2 2)х²= -4

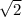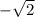х₁= $\sqrt{2}$ ; х₂= $-\sqrt{2}$ х - не имеет ответа.

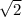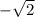ответ: х₁= $\sqrt{2}$ ; х₂= $-\sqrt{2}$ .

в) (х²-16)(х²+2х-8)=0

1) х²-16=0 2) х²+2х-8=0

х²=16 D=(-2)²-4*1*(-8)=36

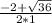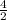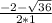х₁=4; х₂= -4. х₃= $\frac{-2+\sqrt{36} }{2*1}$ = $\frac{4}{2}$ =2

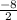х₄= $\frac{-2-\sqrt{36} }{2*1}$ = $\frac{-8}{2}$ = -4

ответ: х₁=4; х₂=х₄= -4; х₃=2

г)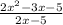 $\frac{2x^{2}-3x-5 }{2x-5}$ =0

2х²-3х-5=0

D=(-3)²-4*2*(-5)=49

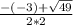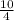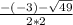х₁= $\frac{-(-3)+\sqrt{49} }{2*2}$ = $\frac{10}{4}$ =2,5

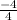х₂= $\frac{-(-3)-\sqrt{49} }{2*2}$ = $\frac{-4}{4}$ = -1

ОДЗ (обще-допустимые значения):

х - не равно 2,5 т.к 2*2,5-5=0, а на ноль делить нельзя.

х= -1.

ответ: х= -1

№2

Пусть x - первое число, тогда х-8 - второе число. Произведение этих чисел равно 105. Составим уравнение:

х*(х-8)=105

х²-8х-105=0

D=(-8)²-4*1*(-105)=484

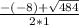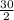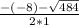х₁= $\frac{-(-8)+\sqrt{484} }{2*1}$ = $\frac{30}{2}$ =15

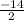х₂= $\frac{-(-8)-\sqrt{484} }{2*1}$ = $\frac{-14}{2}$ = -7

ответ: 15 наибольшее число.

0,0(0 оценок)

Ответ:

Еля2005

02.07.2020 11:42

Решение: Для решения данной задачи введем переменную "Х", через которую обозначим искомую нами скорость моторной лодки. Тогда, по условию задачи, составим следующее уравнение: 10/(Х + 3) + 12/(Х - 3) = 2. Решая данное уравнение, получаем следующее 10 (Х - 3) + 12 (Х + 3) = 2 (Х + 3)(Х - 3) или 10Х - 30 + 12Х + 36 = 2 (Х^2 - 9). В результате сокращений, получаем квадратное уравнение Х^2 -11Х - 12 = 0. Решая квадратное уравнение, получаем два корня -1 и 12. Так как скорость не может быть величиной отрицательной, то скорость моторной лодки будет равна 12 км/ч.

0,0(0 оценок)

Популярные вопросы: Алгебра