С графика найдите: 1) Значение функции, если значение аргумента равно 1; -2;
2) значения аргумента, при которых функция равна -3; 6;
3) значения аргумента, при которых функция приобретает отрицательные значения; положительных значений.
file:///C:/Users/TVOYO/Downloads/saveaspng%20(2).png (График)
1) Уравнение касательной имеет вид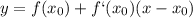
С этого уравнения видно, что коэффициент возле переменной является значением производной функции в точке касания. Найдём же эту точку.
Проведём проверку найденных корней:
Первый корень дал нам уравнение другой касательной,он нам не подходит
Мы нашли абсциссу точки прикосновения, это -2
ответ: х= -2
2) Нужно найти производную функции и приравнять её к нулю, чтобы проверить критические точки на наличие экстремума
Мы нашли стационарную точку х = 3.5 , проверим её на экстремум с метода интервалов.
Подставляю в нашу производную значения с интервалов (подставляем только в числитель, так как знаменатель всегда положителен и мы это доказали выше)
Получаем такие знаки на интервалах:
Видим, что производная при переходе через точку х = 3.5 меняет свой знак с минуса на плюс, что является достаточным условием существования минимума функции в данной точке.
ответ: х = 3.5 - точка минимума функции