с примерами, плз

Представить в виде многочлена (3+8а)^2=

(4в^2-5с^3) ^2=

Разложить на множители

(9а^2+5) (9а^2-5)=

16а^4-25в^6=

Раскрыть скобки

(х+2) (х^2 -2х+4)=

Разложить на множители

х^3 -0,9х^2+0,27х -0,027=

9х^2-2ху+16у^2=

25х^4-20х^2+4=

9/16 -12а^2+64а^4=

Показать ответ

Ответ:

Afon7

03.03.2020 09:43

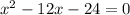
1) x^2 - 12x - 24 = 0

$D = 12^2 - 4\cdot (-24) = 144+4\cdot 24 0$

данное уравнение имеет два различных корня.

по теореме Виета:

x_1 + x_2 = 12

$x_1\cdot x_2 = -24$

Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.

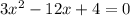
2) 3x^2 - 12x + 4 = 0

$D = 12^2 - 4\cdot 3\cdot 4 = 144 - 4\cdot 12 =144 - 48 0$

уравнение имеет два различных корня.

по теореме Виета:

$x_1 + x_2 = \frac{12}{3} = 4$

$x_1\cdot x_2 = \frac{4}{3}$

Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.

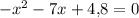
3) $-x^2 - 7x + 4{,}8 = 0$

$D = 7^2 - 4\cdot(-1)\cdot 4{,}8 = 49 + 4\cdot 4{,}8 0$

уравнение имеет два различных корня. По т. Виета:

$x_1 + x_2 = -\frac{-7}{-1} = -7$

$x_1\cdot x_2 = \frac{4{,}8}{-1} = -4{,}8$

Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.

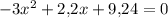
4) $-3x^2 + 2{,}2x + 9{,}24 = 0$

$D = 2{,}2^2 - 4\cdot(-3)\cdot 9{,}24 = 2{,}2^2 + 4\cdot 3\cdot 9{,}24 0$

уравнение имеет два различных корня. По т. Виета:

$x_1+x_2 = -\frac{2{,}2}{-3} = \frac{2{,}2}{3} 0$

$x_1\cdot x_2 = \frac{9{,}24}{-3} < 0$

Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.

0,0(0 оценок)

Ответ:

rodnevadaria

27.03.2021 21:50

Для того, чтобы упростить выражение sk - (4 - sk) + 5sk мы должны открыть скобки, а затем выполнить группировку и приведение подобных слагаемых.

Для открытия скобок применим правило открытия скобок перед которыми стоит знак минус. Мы должны убрать скобки, а знаки слагаемых в скобках сменить на противоположные.

sk - (4 - sk) + 5sk = sk - 4 + sk + 5sk.

В полученном выражении подобными слагаемыми являются sk, sk и 5sk, приведем их и получим выражение:

sk - 4 + sk + 5sk = sk + sk + 5sk - 4 = 7sk - 4.

И ЕЩЕ МАЛЕНЬКАЯ ОТМЕТЬ КАК ЛУЧШЕЕ

0,0(0 оценок)

Популярные вопросы: Алгебра