Одинаковая пропускная означает, что в единицу времени проходит тот же же поток воды. Иными словами совокупная площадь сечений двух исходных труб должна быть равна площади сечения новой трубы. Трубы обычно делают круглыми, значит для расчетов площади сечения мы можем воспользоваться формулами нахождения площади круга. 2*С1 = С2, где С1 - площадь сечения одной из старых труб (они одинаковы, т.к. диаметр одинаков), С2 - площадь сечения новой трубы. С1 = Пи*Д1^2 / 4, С2 = Пи*Д2^2 / 4, где Д1 - диаметр одной из старых труб, Д2 - диаметр новой трубы. 2* Пи*Д1^2 / 4 = Пи*Д2^2 / 4. 2*Д1^2 = Д2^2, Д2 = (2*Д1^2)^1/2. Д2 = 2^1/2 * Д1. (Диаметр новой трубы равен диаметру старой трубы, умноженному на квадратный корень из двух). Значит, при условии, что Д1 = 50, Д2 = 2^1/2 * 50 = [приближенно равно] = 1,414*50 = 70,7.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
Иными словами совокупная площадь сечений двух исходных труб должна быть равна площади сечения новой трубы.
Трубы обычно делают круглыми, значит для расчетов площади сечения мы можем воспользоваться формулами нахождения площади круга.
2*С1 = С2, где С1 - площадь сечения одной из старых труб (они одинаковы, т.к. диаметр одинаков), С2 - площадь сечения новой трубы.
С1 = Пи*Д1^2 / 4,
С2 = Пи*Д2^2 / 4, где Д1 - диаметр одной из старых труб, Д2 - диаметр новой трубы.
2* Пи*Д1^2 / 4 = Пи*Д2^2 / 4.
2*Д1^2 = Д2^2,
Д2 = (2*Д1^2)^1/2.
Д2 = 2^1/2 * Д1.
(Диаметр новой трубы равен диаметру старой трубы, умноженному на квадратный корень из двух).
Значит, при условии, что Д1 = 50,
Д2 = 2^1/2 * 50 = [приближенно равно] = 1,414*50 = 70,7.
Дана функция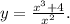
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).