с ускорением сделайте мне очень нужен​

Рассмотрим треугольник ABC, Высота проведённая из вершины С делит треугольник ABC на два равных треугольник (по трём углоам)

Рассмотрим трегольник НСА - прямоугольный (т.к СН высота), по определению cos это отношение прилежащего  катета к гипотенузе, но нам известен противолежащий катет следовательно нам нужно найти синус по основному тригонаметрическому ождеству 1-(sqrt10/10)^2=1-10/100=90/100 => sin=3/sqrt10

6/AC=3/sqrt10

3AC=6sqrt10 |:3

AC=2sqrt10

По теореме Пифагора

AH^2=(2sqrt10)^2-6^2=40-36=4

AH=2

Т.к HBC=HBA, то HB=AH=2

AB=HB+AH=2+2=4

ответ: АВ=4

1. (х+4)(х+6) 2. (х -3)(х - )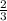

Объяснение:

1. х^2 +10x - 24

a=1, b=10, c=-24

Находим дискриминант и получаем D= 4

формулы x1 =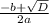 находим первый корень, который равен -4

А с формулы х2=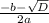 находим второй корень, который равен -6

Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)

Получаем:

x^2+10x-24= 1(x-(-4))(x-(-6)) = (x+4)(x+6)

2. 3x^2-11x+6

a=3, b=-11, c=6

Находим дискриминант и получаем D= 49

формулы x1 =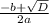 находим первый корень, который равен 3

А с формулы х2=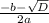 находим второй корень, который равен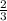

Используем формулу квадратного трёхчлена ax^2+bx+c=a(x-x1)(x-x2)

Получаем:

3x^2-11x+6= 1(x-3)(x-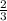 )