Дробь является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
.
Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
Составное число – это число, которое имеет два делителя кроме единицы. Например, составное число 1234 кратно 2, значит делится 2 и минимум на число, которое осталось (1234/2=617, 617/617=1, т.е. два делителя 2 и 617) Составное число 2345 кратно 5, значит тоже имеет минимум 2 делителя (2345/5=469, 469/469=1, т.е. два делителя 5 и 469). Составное число 1023, можно проверить на кратность 3 без калькулятора. Для этого нужно сложить сумму чисел (1+0+2+3=6), если она делится на 3 , значит число кратно 3, если нет (например, число 1013 1+0+1+3=5), то разделить на 3 нельзя.
Рассмотрим вариант А: 1234567890, если вычеркнуть любые 6 цифр должно остаться составное число: 1234 (кратно 2), 2345 (кратно 5), 3456 (кратно 2) - составные числа, имеющие два делителя и более (кроме 1). 4567 - простое число, делится только на 1 и 4567 Вариант А не подходит.
Вариант В: 1023456789 Можно увидеть простое число 4567: 1023456789 Вариант В - не подходит.
Вариант С: 7123456890 7123 (делится на 17), 1234, 2345, 3456, 4568 - составные числа 5689 - простое число Вариант С не подходит
Дробь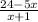
является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
Например, составное число 1234 кратно 2, значит делится 2 и минимум на число, которое осталось (1234/2=617, 617/617=1, т.е. два делителя 2 и 617)
Составное число 2345 кратно 5, значит тоже имеет минимум 2 делителя (2345/5=469, 469/469=1, т.е. два делителя 5 и 469).
Составное число 1023, можно проверить на кратность 3 без калькулятора. Для этого нужно сложить сумму чисел (1+0+2+3=6), если она делится на 3 , значит число кратно 3, если нет (например, число 1013 1+0+1+3=5), то разделить на 3 нельзя.
Рассмотрим вариант А: 1234567890, если вычеркнуть любые 6 цифр должно остаться составное число:
1234 (кратно 2), 2345 (кратно 5), 3456 (кратно 2) - составные числа, имеющие два делителя и более (кроме 1).
4567 - простое число, делится только на 1 и 4567
Вариант А не подходит.
Вариант В: 1023456789
Можно увидеть простое число 4567: 1023456789
Вариант В - не подходит.
Вариант С: 7123456890
7123 (делится на 17), 1234, 2345, 3456, 4568 - составные числа
5689 - простое число
Вариант С не подходит
Остается вариант: D
ОТВЕТ: D) 9713502468