Алгебраическое выражение - это выражение, составленное из букв и чисел, соединенных знаками алгебраических действий: сложения, вычитания, умножения, деления, возведения в степень, извлечения корня.Найти значение алгебраического выражения - это значит найти множество всех его решений.ПОЯСНЕНИЕ. Выражения с переменными - алгебраические.Если в числовом выражении появляются буквы - это выражение становится буквенным выражением. Или выражением с переменными. Или - алгебраическим выражением. Это, практически, одно и то же. Выражение 5а +с, к примеру - и буквенное, и алгебраическое, и выражение с переменными.Почему буквенное - понятно. Ну, раз буквы есть, то любую букву можно заменять на разные числа. Поэтому буквы и называются переменными. В выражении у+5, например, у - переменная величина. Или говорят просто "переменная", без слова "величина". В отличие от цифры пять, например, которая - величина постоянная. Или просто - постоянная.Термин алгебраическое выражение означает, что для работы с данным выражением нужно использовать законы и правила алгебры. Если арифметика работает с конкретными числами, то алгебра - со всеми числами разом. Простой пример для пояснения.В арифметике можно записать, что 3 + 5 = 5 + 3. Посчитать, и все дела.Слева 8, и справа 8. А для других чисел такое равенство выполняется? Тоже можно записать и посчитать. Но чисел - бесконечное количество.. . И что, каждый раз считать? !А вот если мы подобное равенство запишем через алгебраические выражения:а + b = b + aмы сразу решим все вопросы. Для всех чисел махом. Для всего бесконечного количества. Потому, что под буквами а и b подразумеваются все числа. И не только числа, но даже и другие математические выражения. Вот так работает алгебра.
ответ: Уравнение эллипса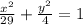
; оси симметрии данного эллипса являются осями координат(или ось Ох и Оу); ε =5/√(29)
Объяснение:
Дан эллипс: F₁ =(-5;0); F₂ =(5;0) и B₁=(0;-2); B₂=(0;2). Напишите уравнение эллипса, найти оси и эксцентриситет
фокусное расстояние эллипса с = 5 (от точки F до точки О)
малая полуось b = 2
большая полуось а находится из соотношения
а² = b² + c²
a² = 2² + 5² = 4 + 25 = 29
уравнение эллипса:
- каноническое уравнение эллипса
Оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии.
Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .
ε = с/ a = 5/√(29)