Алгебра: с заданиями №1, 2, 4.

с заданиями №1, 2, 4.

Показать ответ

Ответ:

Kiberyblydok23

28.01.2023 22:25

Відповідь:

Пояснення:

Якщо цифри в числі можуть повторюватися, то:

на перше місце числа можна поставити будь-яку цифру з трьох: 2, 3, або вибору;

вибір другої і третьої цифр можна здійснити 4-ма (можна вибрати кожну із даних цифр 0, 2, 3, або 5).

Тоді (за правилом добутку) можна утворити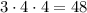 $3\cdot 4\cdot 4=48$ трицифрових чисел.

Якщо цифри в числі не можуть повторюватися, то

на перше місце числа можна поставити будь-яку цифру з трьох: 2, 3, або вибору;

вибір другої цифри можна здійснити теж 3-ма (тут можна поставити і 0);

вибір третьої цифри можна здійснити вже 2-ма .

Тоді (за правилом добутку) можна утворити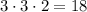 $3\cdot 3\cdot 2=18$ трицифрових чисел.

0,0(0 оценок)

Ответ:

МелодиЛук

24.03.2023 02:05

абсцисса вершины параболы: $m=-\dfrac{p}{2}$ . тогда ординату вершины параболы найдем, подставив абсциссу вершины параболы в график уравнения

$y=\left(-\dfrac{p}{2}\right)^2+p\cdot \left(-\dfrac{p}{2}\right)+q=\dfrac{p^2}{4}-\dfrac{p^2}{2}+q=q-\dfrac{p^2}{4}$

по условию, сумма координат вершины параболы равна 0,5. то есть

$-\dfrac{p}{2}+q-\dfrac{p^2}{4}=\dfrac{1}{2}~~~\bigg|\cdot 4\\ \\ -2p+4q-p^2=2\\ \\ p^2+2p-4q+2=0$

далее парабола пересекает ось ординат в точке с ординатой 0,25, то есть точка (0; 0.25) принадлежит параболе. подставим их координаты

$q=\dfrac{1}{4}$

$p^2+2p-4\cdot \dfrac{1}{4}+2=0$

$p^2+2p+1=0\\ \\ (p+1)^2=0\\ \\ p=-1$

отсюда абсцисса вершины параболы: $m=-\dfrac{p}{2}=\dfrac{1}{2}$

ответ: 0,5.

0,0(0 оценок)

Популярные вопросы: Алгебра

Melissa607

18.01.2022 07:27

Построить схематический чертёж и найти площадь фигуры, ограниченной линиями: y=x^2+mx-n^2, (mn+n^2)x-(m+n)y+m^2n-n^3=0 m=5 n=5...

ajamshid1976p042ct

30.03.2023 05:37

4,5x×8y²×5,16x²y, где х=3, у=1,9...

Тупойшкольник0

07.01.2022 08:50

9. Sayyoh yoʻlning qismini oʻtdi. Hisoblab koʻrsa, yoʻlning yarmiga yetishi uchun yana 9 km yurishi kerak ekan. Say- yoh jami necha kilometr yoʻl yurishni mo ljallagan?...

Ntt1

22.04.2023 13:24

Запишите первые пять членов числовой последовательности заданной рекуррентно: An-1=(-1)^n×An-6,. a1=3...

nocitronum

02.01.2021 22:18

На заводе двое рабочих изготавливают детали. Чтобы изготовить 703 детали первому рабочему нужно на 9 часов меньше, чем второму на изготовление 924 деталей. Известно,...

alexplotnikov201

11.04.2020 14:26

Ваня записал несколько простых чисел использовав ровно по одному разу все цифры от 1 до 9.Сумма этих чисел оказалась равной 225. Можно ли использовав ровно по одному...

luluik

17.09.2020 18:22

Найдите величину α/π+3, где α - радианная мера угла 80o...

dolgunovadaniela

07.07.2020 09:16

Между какими целыми числами заключено число 237/15 1)12 и 13 2)13 и 14 3) 14 и 15 4)15 и 16...

обгрейд

05.07.2020 03:59

вариант 2. ( ) 1. ( ). Постройте график функции: у = 2sin 0,5х. Пользуясь графиком, определите: а) наименьший положительный период функции; б) точки экстремума и экстремумы...

kuklas228

09.05.2023 19:12

Одна из сторон треугольника в 3 раза больше другой и 15 см меньше третьей. найди наименьшую сторону треугольника если его периметр равен 99 см...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку