a) cos(a-b) - cos(a+b) = cos(a)*cos(b) + sin(a)*sin(b) - (cos(a)*cos(b) - sin(a)*sin(b)) = cos(a)*cos(b) + sin(a)*sin(b) - cos(a)*cos(b) + sin(a)*sin(b) = 2sin(a)*sin(b)
b) sin(2a) + cos(2a) + 1 = 2*sin(a)*cos(a) + cos²(a) - sin²(a) + cos²(a) + sin²(a) = 2*sin(a)*cos(a) + 2*cos²(a) = 2*cos(a)*(sin(a) + cos(a))
sin() = -
= arcsin(-) + 2πκ, κ∈Ζ
или
= π - arcsin(-) + 2πn, n∈Ζ
= - + 2πκ, κ∈Ζ
= π + + 2πn, n∈Ζ
= + 2πn, n∈Ζ
x₁ = - + 6πκ, κ∈Ζ
x₂ = + 6πn, n∈Ζ
Отбор корней произведем с неравенств.
x₁: 0 ≤ - + 6πκ ≤ 3π
≤ 6πκ ≤ 3π +
≤ 6πκ ≤
≤ 6κ ≤
≤ κ ≤
Так как κ∈Ζ, то κ∈∅
x₂: 0 ≤ + 6πn ≤ 3π
- ≤ 6πn ≤ 3π -
- ≤ 6πn ≤ -
- ≤ 6n ≤ -
- ≤ n ≤ -
Так как n∈Ζ, то n∈∅ ⇒ нет корней на данном промежутке
a) cos(a-b) - cos(a+b) = cos(a)*cos(b) + sin(a)*sin(b) - (cos(a)*cos(b) - sin(a)*sin(b)) = cos(a)*cos(b) + sin(a)*sin(b) - cos(a)*cos(b) + sin(a)*sin(b) = 2sin(a)*sin(b)
b) sin(2a) + cos(2a) + 1 = 2*sin(a)*cos(a) + cos²(a) - sin²(a) + cos²(a) + sin²(a) = 2*sin(a)*cos(a) + 2*cos²(a) = 2*cos(a)*(sin(a) + cos(a))
sin(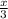 ) = -
) = -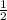
или
x₁ = -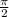 + 6πκ, κ∈Ζ
+ 6πκ, κ∈Ζ
x₂ =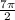 + 6πn, n∈Ζ
+ 6πn, n∈Ζ
Отбор корней произведем с неравенств.
x₁: 0 ≤ -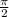 + 6πκ ≤ 3π
+ 6πκ ≤ 3π
Так как κ∈Ζ, то κ∈∅
x₂: 0 ≤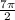 + 6πn ≤ 3π
+ 6πn ≤ 3π
-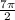 ≤ 6πn ≤ 3π -
≤ 6πn ≤ 3π - 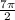
-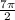 ≤ 6πn ≤ -
≤ 6πn ≤ - 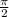
-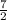 ≤ 6n ≤ -
≤ 6n ≤ - 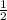
-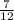 ≤ n ≤ -
≤ n ≤ - 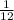
Так как n∈Ζ, то n∈∅ ⇒ нет корней на данном промежутке