Самостоятельная работа по теме:
«построение графика квадратичной функции»
1 вариант
1. найдите координаты вершины параболы.
а) у = х* - 4х + 5 б) у = 2х* - 4х - 6 в) у = -0,5 x® + 3х + 2,5 в) y=-x +2х.
2. постройте график квадратичной функции
а) у = х* - 2х + 1 б) у = -2x*+3x – 4 в) у = 2x* + х +4 в) у = - x® + 3х.
3. постройте график квадратичной функции и опишите ее свойства:
y=(2-x)(х+6)
ЭТО ЗНАК КОРНЯ √
ЗАДАНИЕ 1 10х² =5х+0,6;
10x^2+(-5x-3/5)=0
дискриминант
x1=(√D-b)/2a
x2=(-√D-b)/2a
где D=b^2-4*a*c
так как a=10; b=-5; c=-3/5
D=(-5)^2-4*10*-3/5=49
√49 = 7
x1=(7-(-5))/2*10
x1=12/20
x1=0.6=3/5
x2=(-7-(-5))/2*10
x2=-2/20
x2=-0.1=1/10
ЗАДАНИЕ 2 х²+3+4х=0 (если я правильно понял)
a=1
b=4
c=3
D=4^2-4*1*3=4
x1=-3
x2=-1
ЗАДАНИЕ 3 х²+5х=-6; x2+5x+6=0
a=1
b=5
c=6
D=5^2-4*1*6=1
x1=-3
x2=-2
ЗАДАНИЕ 4 1-4х=5х²; -5х²+(1-4х)=0;
a=-5
b=-4
c=1
D=(-4)^2-4*(-5)*1=36
x1=-1
x2=1/5
ЗАДАНИЕ 5 81у²+1=-18у; 18y+(81y^2+1)=0
a=81
b=18
c=1
D=18^2-4*81+1=0
y1=-1/9
ЗАДАНИЕ 6 3р= 5р²-2; 3p+(2-5p^2)=0
a=-5
b=3
c=2
D=3^2-4*(-5)*2=49
p1=-2/5
p2=1
1. x₁ = -10; x₂ = 9
2. х₁ = 8; x₂ = 6
Объяснение:
1. Решаем через дискриминант:
х²+х-90=0;
D = b²- 4ac (формула дискриминанта)
D = 1² - 4 · 1 · (-90) = 1 + 360 = 361 (Дискриминант больше нуля (361 > 0) значит у уравнения 2 корня)
√361 = 19
х₁ =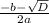
x₁ =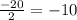
х₂ =
x₂=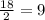
x₁ = -10; x₂ = 9
2. Решаем через дискриминант:
х²-10х-24=0
D = b²- 4ac (формула дискриминанта)
D = -10² - 4 · 1 · 24 = 100 - 96 = 4 (Дискриминант больше нуля (4 > 0) значит у уравнения 2 корня)
√4 = 2
х₁ =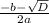
х₁ =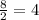
х₂ =
х₂ =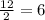
х₁ = 8; x₂ = 6
Надеюсь с: (Если что не понял пиши в комменты)