Самостоятельная работа по теме « Статистические характеристики Вариант 1
А1. Найдите медиану ряда чисел 24,3; 11,2; 13,3; 21,0; 11,2.
1) 16,2 2) 16,0 3) 13,3 4) 11,2
А2. Найдите среднее арифметическое ряда чисел 26,5; 8,6; 26,5; 13,0; 6,4.
1) 26,5 2) 20,1 3) 16,2 4) 13,0
А3. Ряд чисел дополнили числом, которое меньше всех остальных его чисел. Как могут измениться размах и мода этого ряда?
1) размах и мода не изменятся
2) размах увеличится, а мода не изменится
3) размах и мода уменьшатся
4) размах не изменится, а мода увеличится
В1. Среднее арифметическое ряда, состоящего из 9 чисел, равно 20. Из этого ряда вычеркнули число 12. Найдите среднее арифметическое получившегося ряда.
С1. В магазин привезли 20 ящиков яблок со средней массой яблока 250 г, а также 30 ящиков яблок со средней массой плода 230 г. Найдите среднюю массу яблока во всей партии, если количество яблок в каждом ящике одно и то же.
По условию: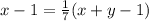
.
Получаем первое уравнение:
Ещё по условию: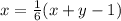
.
Второе уравнение:
Левые части обоих уравнений равны, значит, их правые части равны между собой.
Подставим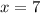
в уравнение 
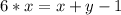и получим:
ответ: 7 красныx;
36 жёлтых;
43 всего шаров в коробке.
2,5
Объяснение:
Обозначим скорость Лады L км/ч, а скорость Мерседеса M км/ч.
Путь обозначим AB = S км. Так как они встретились через 8 ч, то:
M + L = S/8
Если бы скорость Мерседеса была 1,14M км/ч, а скорость Лады 1,15L км/ч, то они встретились бы через 7 ч:
1,14M + 1,15L = S/7
Получили систему, в которой 2 уравнения и 3 неизвестных.
Умножаем 1 уравнение на 8, а 2 уравнение на 7
{ 8M + 8L = S
{ 7,98M + 8,05L = S
Правые части равны, приравниваем левые части друг к другу.
8M + 8L = 7,98M + 8,05L
8M - 7,98M = 8,05L - 8L
0,02M = 0,05L
2M = 5L
M : L = 5/2 = 2,5