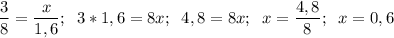Дано неравенство.Линейная функция (3-х) убывающая, а показательная (3^х) возрастающая для всех х€R.
При х=0 3>1-неравенство не выполняется, значит возможные решения лежат в интервалах 2 и 4.
При х=0.7 2.3>2.158 -неравенство не выполняется, значит х=0.7 и бесконечно близкие к нему значения не входят в область решений. Возьмем х=0.74, получим 2.26>2.255 -опять не выполняется, а при х=0.742 2.258<2.260 -выполняется. Значит нижней границей интервала значение х=0.7 не является, поскольку при значениях 0.7<х<0.74 (например) неравенство не выполняется.
На 4м интервале неравенство верное для всех х этого интервала, включая даже х=2.3
четвертое х€(2,3;∞)
Объяснение
Дано неравенство.Линейная функция (3-х) убывающая, а показательная (3^х) возрастающая для всех х€R.
При х=0 3>1-неравенство не выполняется, значит возможные решения лежат в интервалах 2 и 4.
При х=0.7 2.3>2.158 -неравенство не выполняется, значит х=0.7 и бесконечно близкие к нему значения не входят в область решений. Возьмем х=0.74, получим 2.26>2.255 -опять не выполняется, а при х=0.742 2.258<2.260 -выполняется. Значит нижней границей интервала значение х=0.7 не является, поскольку при значениях 0.7<х<0.74 (например) неравенство не выполняется.
На 4м интервале неравенство верное для всех х этого интервала, включая даже х=2.3
а) b = 18 б) b = 10 в) y=20 г) y = 1,2
д) a = 9 е) a = 24 ж) x = 1,4 з) x = 0,6
Объяснение:
Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции.
a : b = c : d ⇒ ad = bc
а) 2 : 9 = 4 : b; 2b = 9*4; 2b = 36; b = 36 : 2; b = 18;
б) 15 : b = 3 : 2; 15*2 = b*3; 30 = 3b; b = 30 : 3; b = 10;
в) 3 : 2,1 = y : 14; 3 * 14 = 2,1y; 42 = 2,1y; y = 42 : 2,1; y = 20;
г) y : 2,4 = 3 : 6; 6y = 2,4*3; 6y = 7,2; y = 7,2 :6; y = 1,2;
д)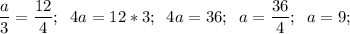
е)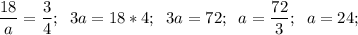
ж)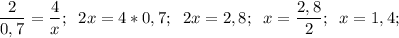
з)