Дано: ΔABC равнобедренный; AB = BC; BO высота; BN = BM.
Доказать: NO = MO.
Доказательство:
ΔBNO = ΔBMO по 1 признаку равенства треугольников (по двум сторонам и углу между ними).
BN = BM по условию;
BO общая сторона;
∠NBO = MBO, т.к. высота в равнобедренном треугольнике является медианой и биссектрисой. Высота BO является биссектрисой ∠NBM, т.е. делит его на на два равных угла.
Из равенства треугольников следует равенство соответствующих сторон. NO = MO, что и требовалось доказать.
Перепишем уравнение эллипса, поменяв местами параметры и :
При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.
Найдём эксцентриситет:
Найдём фокальное расстояние (полурасстояние между фокусами):
Тогда расстояние между фокусами в два раза больше: .
ответ: 6 ед.
На чертеже изображён данный эллипс. и — его фокусы.
Дано: ΔABC равнобедренный; AB = BC; BO высота; BN = BM.
Доказать: NO = MO.
Доказательство:
ΔBNO = ΔBMO по 1 признаку равенства треугольников (по двум сторонам и углу между ними).
BN = BM по условию;
BO общая сторона;
∠NBO = MBO, т.к. высота в равнобедренном треугольнике является медианой и биссектрисой. Высота BO является биссектрисой ∠NBM, т.е. делит его на на два равных угла.
Из равенства треугольников следует равенство соответствующих сторон. NO = MO, что и требовалось доказать.
Рисунок в приложении.
Каноническое уравнение, задающее эллипс, выглядит так:
Перепишем уравнение эллипса, поменяв местами параметры
и 
:
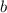При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.
Найдём эксцентриситет:
Найдём фокальное расстояние (полурасстояние между фокусами):
Тогда расстояние между фокусами в два раза больше: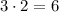
.
ответ: 6 ед.
На чертеже изображён данный эллипс.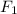
и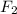 
— его фокусы.