Объяснение:
1) нарисуйте круг радиусом 8 м (диаметр 16 м < 20 м, на участке поместится целиком) и поставьте на нем 6 точек через равные расстояния.
Это расстояние у правильного 6-угольника = радиусу, то есть 8 м.
Более того, можно поставить седьмое дерево в центр круга, и оно тоже будет на расстоянии 8 м (радиус) от любого дерева на окружности.
2) Смотрим 1 упаковку.
1+5+8 = 14, счастливыми будут билеты:
158419, 158428, 158437, 158446, 158455, 158464, 158473, 158482, 158491, 158509, 158518, 158527, 158536, 158545, 158554, 158563, 158572, 158581, 158590 - 19 билетов.
Смотрим 2 упаковку
2+5+6 = 13, счастливыми будут билеты:
256229, 256238, 256247, 256256, 256265, 256274, 256283, 256291, 256319, 256328, 256337, 256346, 256355, 256364, 256373, 256382, 256391 - 17 билетов.
Смотрим 3 упаковку
4+6+2 = 12, счастливыми будут билеты:
462039, 462048, 462057, 462066, 462075, 462084, 462093, 462129, 462138, 462147, 462156, 462165, 462174, 462183, 462192 - 15 билетов.
Самая счастливая - 1 упаковка.
Пусть случайная величина X - число выбитых очков; также добавим что эта случайная величина распределена по биномиальному закону.
1) Стрелок выбил 0 очков, т.е. он не попал ни разу в мишень. Такова вероятность будет
2) Стрелок выбил 5 очков, т.е. в мишень он попал один раз. Вероятность того, что при 4 выстрелах стрелок попадет только один раз, равна
3) Стрелок выбил 10 очков, т.е. в мишень он попадает два раза. Вероятность того, что при четырех выстрелах стрелок попадет ровно два раза равна
4) Стрелок выбил 15 очков, т.е. в мишень стрелок попал три раза. Вероятность того, что при 4 выстрелах стрелок попал ровно 3 раза равна
5) Стрелок выбил 20 очков, т.е. он в мишень попал ровно 4 раза. Такова вероятность
Закон распределения случайной величины X:
Xi 0 5 10 15 20
Pi 0.09150625 0.299475 0.3675375 0.200475 0.04100625
Объяснение:
1) нарисуйте круг радиусом 8 м (диаметр 16 м < 20 м, на участке поместится целиком) и поставьте на нем 6 точек через равные расстояния.
Это расстояние у правильного 6-угольника = радиусу, то есть 8 м.
Более того, можно поставить седьмое дерево в центр круга, и оно тоже будет на расстоянии 8 м (радиус) от любого дерева на окружности.
2) Смотрим 1 упаковку.
1+5+8 = 14, счастливыми будут билеты:
158419, 158428, 158437, 158446, 158455, 158464, 158473, 158482, 158491, 158509, 158518, 158527, 158536, 158545, 158554, 158563, 158572, 158581, 158590 - 19 билетов.
Смотрим 2 упаковку
2+5+6 = 13, счастливыми будут билеты:
256229, 256238, 256247, 256256, 256265, 256274, 256283, 256291, 256319, 256328, 256337, 256346, 256355, 256364, 256373, 256382, 256391 - 17 билетов.
Смотрим 3 упаковку
4+6+2 = 12, счастливыми будут билеты:
462039, 462048, 462057, 462066, 462075, 462084, 462093, 462129, 462138, 462147, 462156, 462165, 462174, 462183, 462192 - 15 билетов.
Самая счастливая - 1 упаковка.
Пусть случайная величина X - число выбитых очков; также добавим что эта случайная величина распределена по биномиальному закону.
1) Стрелок выбил 0 очков, т.е. он не попал ни разу в мишень. Такова вероятность будет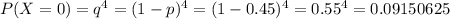
2) Стрелок выбил 5 очков, т.е. в мишень он попал один раз. Вероятность того, что при 4 выстрелах стрелок попадет только один раз, равна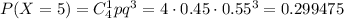
3) Стрелок выбил 10 очков, т.е. в мишень он попадает два раза. Вероятность того, что при четырех выстрелах стрелок попадет ровно два раза равна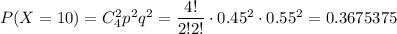
4) Стрелок выбил 15 очков, т.е. в мишень стрелок попал три раза. Вероятность того, что при 4 выстрелах стрелок попал ровно 3 раза равна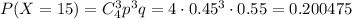
5) Стрелок выбил 20 очков, т.е. он в мишень попал ровно 4 раза. Такова вероятность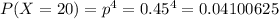
Закон распределения случайной величины X:
Xi 0 5 10 15 20
Pi 0.09150625 0.299475 0.3675375 0.200475 0.04100625