Составляем уравнение времени движения: . Приводим к общему знаменателю и получаем квадратное уравнение: 9х² - 24х -9 = 0, или, сократив на 3: 3х² - 8х - 3 = 0. Квадратное уравнение, решаем относительно x: Ищем дискриминант: D=(-8)^2-4*3*(-3)=64-4*3*(-3)=64-12*(-3)=64-(-12*3)=64-(-36)=64+36=100;Дискриминант больше 0, уравнение имеет 2 корня: x₁=(√100-(-8))/(2*3)=(10-(-8))/(2*3)=(10+8)/(2*3)=18/(2*3)=18/6=3;x₂=(-√100-(-8))/(2*3)=(-10-(-8))/(2*3)=(-10+8)/(2*3)=-2/(2*3)=-2/6=-(1/3)≈-0.3333 это отрицательное значение отбрасываем. ответ: скорость катера равна 3 км/час.
Приводим к общему знаменателю и получаем квадратное уравнение:
9х² - 24х -9 = 0, или, сократив на 3:
3х² - 8х - 3 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-8)^2-4*3*(-3)=64-4*3*(-3)=64-12*(-3)=64-(-12*3)=64-(-36)=64+36=100;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√100-(-8))/(2*3)=(10-(-8))/(2*3)=(10+8)/(2*3)=18/(2*3)=18/6=3;x₂=(-√100-(-8))/(2*3)=(-10-(-8))/(2*3)=(-10+8)/(2*3)=-2/(2*3)=-2/6=-(1/3)≈-0.3333 это отрицательное значение отбрасываем.
ответ: скорость катера равна 3 км/час.
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)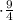
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: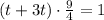
9t = 1
Значит,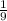
- цис./ч - производительность "медленного" насоса.
Тогда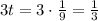
- цис./ч - производительность "быстрого" насоса.
Следовательно,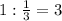
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.