Сделайте номер 3,4,10 со скринов

Больше не добавляйте вопрос в котором больше 3 пример так как дальше можно отметить "Много решений".

x³+4x²-x-4=0

x²*(x+4)-(x+4)=0

x+4)*(x²-1)=0

x+4=0

x²-1=0

x=-4

x=-1

x=1

x₁=-4, x₂=-1, x₃=1

______________

x³-2x²-15x=0

x*(x²-2x-15)=0

x*(x²+3x-5x-15)=0

x*(x*x+3)-5(x+3))=0

x*(x+3)*(x-5)=0

x=0

x+3=0

x-5=0

x=0

x=-3

x=5

x₁=-3, x₂=0, x₃=5

_____________

(2x-5)²*(x-5)=(2x-5)*(x-5)²

(2x-5)²*(x-5)-(2x-5)*(x-5)²=0

(2x-5)*(x-5)*(2x-5-x(x-5))=0

(2x-5)*(x-5)*(2x-5-x+5)=0

(2x-5)*(x-5)x=0

2x-5=0

x-5=0

x=0

x=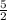

x=5

x=0

x₁=0, x₂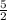,x₃=5

Альтернативная форма:

x₁=0, x₂=2,5, x₃=5

______________

(x-1)*(x²+8x+16)=6(x+4)

x³+8x²+16x-x²-8x-16=6x+24

x³+7x²+8x-16=6x+24

x³+7x²+8x-16-6x-24=0

x³-2x²+9x²+2x-40=0

x³-2x²+9x²-18x+20x-40=0

x²*(x-2)+9x*(x-2)+20(x-2)=0

(x-2)*(x²+9x+20)=0

(x-2)*(x²+5x+4x+20)=0

(x-2)*(x*(x+5)+4(x+5))=0

(x-2)*(x+5)*(x+4)=0

x-2=0

x+5=0

x+4=0

x=2

x=-5

x=-4

x₁=-5, x₂=-4, x₃=2

______________

x⁴=(4x-5)²

x²=|4x-5|

x²-|4x-5|=0

x²-(4x-5)=0 , 4x-5≥0

x²-(-(4x-5))=0 , 4x-5<0

x∉R,x≥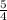

x=-5

        ,x<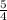

x=1

x∉R

x=-5

x=1

x₁=-5, x₂=1

Если мой ответ вас устраивает выбрать его наилучшим

1

Объяснение:

Вообще решается двумя аналитическим и алгебраическим.

1) аналитический

x >= -8 и x <= 5 - ОДЗ

подставляя, мы получаем. Что единственный корень x = 1.

2) алгебраический

sqrt(8+x) - sqrt(5-x) = 1

возводим в квадрат  обе части

8+x - 2sqrt(-x^2-3x+40) + 5-x=1

преобразовываем:

sqrt(-x^2-3x+40) = 6

решаем квадратное уравнение

-x^2-3x+4=0

D = 9+16 = 25

x1 = (3+5)/-2 = -4

x2 = (3-5)/-2 = 1

При проверке получается:

x1 = -4 - не подходит

sqrt(4) - sqrt(9) = 1

2 - 3 = 1

-1 != 1

x2 = 1 - подходит

sqrt(9) - sqrt(4) = 1

3 - 2 = 1

1 = 1