Знаменатель дроби не должен быть равен нулю. Получаем:
Чтобы это решить, для начала представим, что это выражение равно нулю, тогда получим квадратное уравнение и найдём его корни.
Но так как изначально это выражение было неравно нулю, то из области определения просто вычёркиваются корни уравнения, решённого нами выше.
ответ: .
б)
Подкоренное выражение всегда неотрицательно, то есть, больше или равно нулю.
Решим неравенство методом интервалов.
Нули:
- + -
-----------------------------------------------
Нам нужно найти те промежутки, где выражение больше или равно нулю. Такой промежуток только один: , так как там "+". Этот промежуток и будет являться областью определения функции.
а)
Знаменатель дроби не должен быть равен нулю. Получаем:
Чтобы это решить, для начала представим, что это выражение равно нулю, тогда получим квадратное уравнение и найдём его корни.
Но так как изначально это выражение было неравно нулю, то из области определения просто вычёркиваются корни уравнения, решённого нами выше.
ответ: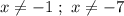 .
.
б)
Подкоренное выражение всегда неотрицательно, то есть, больше или равно нулю.
Решим неравенство методом интервалов.
Нули: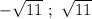
- + -
--------------------- --------------------------
--------------------------
Нам нужно найти те промежутки, где выражение больше или равно нулю. Такой промежуток только один:![[-\sqrt{11}\ ;\ \sqrt{11}]](/tpl/images/1574/8115/b27f8.png) , так как там "+". Этот промежуток и будет являться областью определения функции.
, так как там "+". Этот промежуток и будет являться областью определения функции.
ответ:![x \in [-\sqrt{11}\ ;\ \sqrt{11}]](/tpl/images/1574/8115/4aef2.png) .
.
Объяснение:
первый член х,второй хq,третий хq²,
хq²-хq = разности арифметической последовательности.
значит четвертый член хq²+хq²-хq=2хq²-хq
Сумма всех 4 членов 39= х+ хq+ хq²+2хq²-хq
39= х+ 3хq² =х(1+3q²)
сумма второго и третьего равна хq+ хq²=18 , х=18/(q+ q²)
39= (1+3q²) *18/(q+ q²)
39q+39 q²=18+54q²
0=15q²-39q+18 :3
0=5q²-13q+6
q=13±√(169-120) / 10
q₁≠(13+7)/10 так как прогрессия убывающая, q∠1
q₂=(13-7)/10 q=0,6 х=18/(0,6+0,36)= 18.75
18.75 литров в первом.
18,75*0,6=11,25 литров во втором.
11,25*0,6=6,75 литров в третьем.
6,75-11,25= - 4,5 это разность арифметической.
6,75-4,5=2,25литра в четвертом
проверка. 2,25+6,75+11,25+18,75=39