Середины сторон прямоугольника АВСD являются вершинами четырехугольника MNPK. Периметр прямоугольника равен 40 см, одна сторона в три раза больше другой. Из прямоугольника случайным образом выбирается точка. Найдите вероятность того, что она принадлежит четырехугольнику MNPK.
Противоположные углы параллелограмма равны. Так как сумма всех углов в параллелограмме равна 360 градусов, а противоположные углы между собой равны, то угол, принадлежащий одной стороне с данным, равен (360 – 2Х)/2. Выполняем действие и получаем 180 - Х. Таким образом в параллелограмме два угла равны Х, а два других угла равны 180 - Х. .Обозначим через Х один угол,тогда другой будет Х+40. Составляем уравнение:
(х+40) + (х+40) + х + х = 360
х + 40 + х +40 + х + х = 360
4х = 360 - 40 - 40
4х = 280
х = 70
Отсюда следует, что два угла по 70 градусам и оставшиеся два по 110.
Проверяем: 70+70+110+110 = 360
ответ:110
1) 11
2) 4
Объяснение:
1) 20 + 8х - х² > 0
- х²+8x+20 = 0
D = 64+80 = 144 =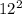
x1 =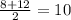 x2 =
x2 = 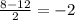
- -2 + 10 -
Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î
Нам подходит промежуток (-2; 10)
Определим целые числа в промежутке: -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Всего целых решений: 11
2) 4x² - 17x + 4 ≤ 0
4x² - 17x + 4 = 0
D = 289-64 = 225 =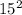
x1 =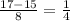 x2 =
x2 = 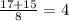
+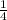 - 4 +
- 4 +
Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î
Нам подходит промежуток [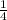 ; 4]
; 4]
Определим целые числа в промежутке: 1, 2, 3, 4
Всего целых решений: 4