Сергей Петрович решил построить на дачном участке теплицу длиной 11м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 10м каждая и покрытие для обтяжки. Отдельно требуется купить плёнку для передней и задней стенок теплицы . Внутри теплицы Сергей Петрович планирует сделать 3 грядки по длине теплицы - 1 центральную широкую грядки 2 узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25 см × 25 см. Высота теплицы показана на рисунке отрезком HF
1.Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?
2.Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продается упаковками по 12 штук?
3. Найдите высоту теплицы. ответ дайте в метрах с точностью до десятых.
4. Найдите ширину узкой грядки, если ширина Центральной грядки в два раза больше ширины узкой грядки. ответ дайте в сантиметрах с точностью до десятых.
5. Сколько квадратных метров пленки необходимо купить для передней и задней стенок, если с учетом крепежа её нужно брать с запасом 10% ? ответ округлите до десятых
Система уравнгений:
{ x ^ 2 + y ^ 2 = 5;
x - y = 1;
{ x ^ 2 + y ^ 2 = 5;
x = 1 + y;
{ (1 + y) ^ 2 + y ^ 2 = 5;
x = 1 + y;
{ 1 + 2 * y + y ^ 2 + y ^ 2 = 5;
x = 1 + y;
{ 2 * y ^ 2 + 2 * y + 1 = 5;
x = 1 + y;
{ 2 * y ^ 2 + 2 * y + 1 - 5 = 0;
x = 1 + y;
{ 2 * y ^ 2 + 2 * y - 4 = 0;
x = 1 + y;
{ 2 * (y ^ 2 + y - 2) = 0;
x = 1 + y;
Найдем корни квадратного уравнения чеез дискриминант:
y ^ 2 + y - 2 = 0;
D = b ^ 2 - 4 * a * c = 1 - 4 * 1 * (- 2) = 9;
y1 = (- 1 + 3)/2 = 2/2 = 1;
y2 = (- 1 - 3)/2 = - 4/2 = - 2;
Тогда:
x1 = 1 + y1 = 1 + 1 = 2;
x2 = 1 + (- 2) = 1 - 2 = - 1;
ответ: (2; 1) и (- 1; - 2).
Объяснение:
№1
а) √50 > 7
√50 > √7²
√50 > √49
б) 4√6 > 3√7
√4²*6 > √3²*7
√16*6 > √9*7
√96 > √63
№2
а) √(196 * 0,64) = √(14²*(0,8)²) = 14 * 0,8 = 11,2
б) √(72*0,5)=√36=√6² = 6
в)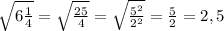
г) √(-2)⁶ = √((-2)³)²=(-2)³= - 8
№3
а) (√3+√2)² = (√3)²+ 2 *√3*√2 + (√2)²= 3 + 2√6 + 2 = 5 +2√6
б) (4 - √5)(4 + √5) = 4² - (√5)² = 16 - 5 = 11
в) 5√12 - 2√27 - 3√3 = 5√(4*3) - 2√(9*3) - 3√3 = 5√(2²*3) - 2√(3²*3) - 3√3 = 5*2√3 - 2*3√3 - 3√3= 10√3 - 6√3 - 3√3 = √3
№4
√(72*а⁵) = √(36*2 * а⁴*а)= √(6²*2 * (а²)² * а) = 6*а²*√(2а)
№5
№6