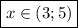Шкільний Спортивний Майнчик прямокут форми має довжину 41,5 а ширину 27,5 , стежка вздовж спортивного майданчика має зовнішній периметр 154м Знайдіть ширину стежки даю 20 Б
Координаты точки пересечения графиков функций (4/3; 2/3)
Решение системы уравнений (4/3; 2/3)
Объяснение:
Решите систему уравнений графически
y=2x-2
y=x/2
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y=2x-2 y=x/2
Таблицы:
х -1 0 1 х -2 0 2
у -4 -2 0 у -1 0 1
Координаты точки пересечения графиков функций (4/3; 2/3)
Вот это уже хорошо. Нужно, чтобы это выражение было меньше единицы (это из признака Даламбера), тогда мы найдем те самые х, при которых ряд будет сходиться.
Вот мы их получили. Но теперь нужно проверить концы:
Что можно сказать об этом ряде? Допустим, мы будем использовать предельный признак сравнения. Есть известный ряд , он расходится, при этом предел отношения n-ых членов полученного ряда и приведенного не равен 0, а равен конкретной константе (-1/2, если делить n-ый член полученного на n-ый член ряда 1/n), так что при ряд расходится.
Аналогичная история
Все те же рассуждения, только предел отношения будет равен 1/2. То есть при ряд расходится.
Координаты точки пересечения графиков функций (4/3; 2/3)
Решение системы уравнений (4/3; 2/3)
Объяснение:
Решите систему уравнений графически
y=2x-2
y=x/2
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y=2x-2 y=x/2
Таблицы:
х -1 0 1 х -2 0 2
у -4 -2 0 у -1 0 1
Координаты точки пересечения графиков функций (4/3; 2/3)
Решение системы уравнений (4/3; 2/3)
Итак, у нас есть ряд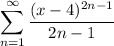 .
.
Вычислим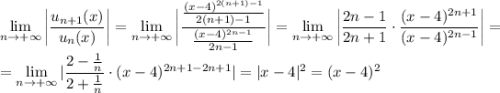
Вот это уже хорошо. Нужно, чтобы это выражение было меньше единицы (это из признака Даламбера), тогда мы найдем те самые х, при которых ряд будет сходиться.
Вот мы их получили. Но теперь нужно проверить концы: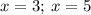
Что можно сказать об этом ряде? Допустим, мы будем использовать предельный признак сравнения. Есть известный ряд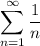 , он расходится, при этом предел отношения n-ых членов полученного ряда и приведенного не равен 0, а равен конкретной константе (-1/2, если делить n-ый член полученного на n-ый член ряда 1/n), так что при
, он расходится, при этом предел отношения n-ых членов полученного ряда и приведенного не равен 0, а равен конкретной константе (-1/2, если делить n-ый член полученного на n-ый член ряда 1/n), так что при 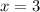 ряд расходится.
ряд расходится.
Аналогичная история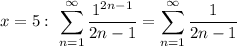
Все те же рассуждения, только предел отношения будет равен 1/2. То есть при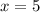 ряд расходится.
ряд расходится.
ответ: