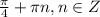Переходим к одному аргументу:
Тогда уравнение можно записать в виде:
Переносим все слагаемые влево и раскладываем на множители группировки:
или
О т в е т ;
Переходим к одному аргументу:
Тогда уравнение можно записать в виде:
Переносим все слагаемые влево и раскладываем на множители группировки:
О т в е т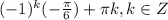 ;
;