Две бригады, работая вместе выполняют некоторую работу за 2 дня. За сколько дней эту работу выполнила бы каждая бригада в отдельности, если первой бригаде на это нужно на 3 дня больше, чем второй?
Решение.
Пусть за дней всю работу выполнила бы первая бригада, тогда
за дней всю эту работу выполнила бы вторая бригада.
Примем весь объём работы за 1 (единицу), тогда
- производительность первой бригады;
- производительность первой бригады.
- общая производительность двух бригад.
Уравнение:
(
не удовлетворяет условию, т.к.
удовлетворяет условию.
За 6 дней всю работу выполнила бы первая бригада.
За 6-3=3 дня всю эту работу выполнила бы вторая бригада.
Позначимо одноцифрове число як - А. Якщо одноцифрове число А збільшити на 10 одиниць, то утвориться двоцифрове число ( 10 + А ). У такому випадку число А збільшується на ( ( 10 + А ) - А ) / А × 100% = 1000 / А %, або у ( 1 + 10 / А ) разів.
За умовами задачі подвійне послідовне збільшення числа А на однакову величину перетворило його на число 72. Маємо рівняння:
А × ( 1 + 10 / А ) × ( 1 + 10 / А ) = 72
Розділимо обидві частини рівняння на А та зробимо заміну:
Х = 1 / А
Відповідно:
А = 1 / Х
Отримуємо:
1 + 20Х + 100Х^2 = 72Х
100Х^2 - 52Х + 1 = 0
Дискріменант рівняння дорівнює:
D = (-52)^2 - 4 × 100 × 1 = 2304
Корні рівняння дорівнюєть:
Х1 = ( 52 + 48 ) / ( 2 × 100 ) = 0,5
Х2 = ( 52 - 48 ) / ( 2 × 100 ) = -0,02
Відповідно маємо:
А1 = 1 / 0,5 = 2
А2 = 1 / ( -0,02 ) = -50
Другий корінь відкидаємо, бо за умовою задачі число А - одноцифрове.
Перевірка:
Число 2 збільшили на 10 одиниць - утворилось число 10 + 2 = 12. У такому випадку число 2 збільшилось на ( 12 - 2 ) / 2 × 100% = 500 %, або у ( 1 + 10 / 2 ) = 6 разів. Також можна сказати, що збільшене число складає ( 1 + 10 / 2 ) × 100% = 600% від початкового.
За умовами задачі подвійне послідовне збільшення числа 2 у 6 разів перетворило його на число 72.
Две бригады, работая вместе выполняют некоторую работу за 2 дня. За сколько дней эту работу выполнила бы каждая бригада в отдельности, если первой бригаде на это нужно на 3 дня больше, чем второй?
Решение.
Пусть за
дней всю работу выполнила бы первая бригада, тогда
за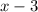
дней всю эту работу выполнила бы вторая бригада.
Примем весь объём работы за 1 (единицу), тогда
Уравнение:
За 6 дней всю работу выполнила бы первая бригада.
За 6-3=3 дня всю эту работу выполнила бы вторая бригада.
ответ: 6 дней; 3 дня.
Відповідь:
Початкове число 2.
Пояснення:
Позначимо одноцифрове число як - А. Якщо одноцифрове число А збільшити на 10 одиниць, то утвориться двоцифрове число ( 10 + А ). У такому випадку число А збільшується на ( ( 10 + А ) - А ) / А × 100% = 1000 / А %, або у ( 1 + 10 / А ) разів.
За умовами задачі подвійне послідовне збільшення числа А на однакову величину перетворило його на число 72. Маємо рівняння:
А × ( 1 + 10 / А ) × ( 1 + 10 / А ) = 72
Розділимо обидві частини рівняння на А та зробимо заміну:
Х = 1 / А
Відповідно:
А = 1 / Х
Отримуємо:
1 + 20Х + 100Х^2 = 72Х
100Х^2 - 52Х + 1 = 0
Дискріменант рівняння дорівнює:
D = (-52)^2 - 4 × 100 × 1 = 2304
Корні рівняння дорівнюєть:
Х1 = ( 52 + 48 ) / ( 2 × 100 ) = 0,5
Х2 = ( 52 - 48 ) / ( 2 × 100 ) = -0,02
Відповідно маємо:
А1 = 1 / 0,5 = 2
А2 = 1 / ( -0,02 ) = -50
Другий корінь відкидаємо, бо за умовою задачі число А - одноцифрове.
Перевірка:
Число 2 збільшили на 10 одиниць - утворилось число 10 + 2 = 12. У такому випадку число 2 збільшилось на ( 12 - 2 ) / 2 × 100% = 500 %, або у ( 1 + 10 / 2 ) = 6 разів. Також можна сказати, що збільшене число складає ( 1 + 10 / 2 ) × 100% = 600% від початкового.
За умовами задачі подвійне послідовне збільшення числа 2 у 6 разів перетворило його на число 72.
2 × ( 1 + 10 / 2 ) = 2 × 6 = 12
12 × ( 1 + 10 / 2 ) = 12 × 6 = 72
Все вірно.