Алгебра: Система уравнений (3 и 4 не решать)

Система уравнений (3 и 4 не решать)

Показать ответ

Ответ:

Софи1138

14.04.2023 20:40

Не самая стандартная задача. Если я правильно понимаю, то имеется в виду, на отрезке [a;b] область значений параболы должна принадлежать отрезку [6;12] .

Для удобства построим график функции

$\displaystyle y=x^2-3x+2=x^2-2\cdot \frac{3}{2}x+\frac{9}{4}-\frac{1}{4}=(x-1.5)^2-0.25$

Парабола, которая смещена по ОХ на 1.5 ед вправо и на 0.25 ед вниз по ОУ. Можно ещё найти точки пересечения с осями. С ОУ совсем просто: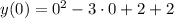 $y(0)=0^2-3\cdot 0+2+2$ , то есть (0;2), для ОХ решим уравнение:

$\displaystyle x^2-3x+2=0 \Rightarrow x^2-x-2x+2=0 \Rightarrow x(x-1)-2(x-1)=0 \Rightarrow \\ \Rightarrow (x-1)(x-2)=0 \Rightarrow \left [ {{x=1} \atop {x=2}} \right.$

То есть точки (1;0); (2;0), при необходимости можно ещё вычислить.

Также построим прямые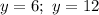 $y=6; \ y=12$

И вот что заметим: вершины параболы внутри отрезка [6;12] по ОУ даже близко не видно, то есть функция там монотонно возрастает или убывает в зависимости от ветви параболы. А значит, наибольшая разность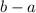 b-a достигается только в том случае, когда областью значений на [a;b] является отрезок [6;12] . Ветвей две и таких отрезка два, проверим оба (хотя очень похоже, что будут одинаковые разности из-за симметрии картинки).

Необходимо решить два уравнения:

$x^2-3x+2=6 \\ x^2-3x+2=12$

Минимальные решения с обоих уравнений пойдут в одну пару [a_1; b_1] , максимальные решения с обоих уравнений пойдут в другую пару [a_2;b_2]

$\displaystyle x^2-3x+2=6 \Rightarrow x^2-3x-4=0 \Rightarrow x^2+x-4x-4=0 \Rightarrow \\ \Rightarrow x(x+1)-4(x+1)=0 \Rightarrow (x+1)(x-4)=0 \Rightarrow \left [ {{x=-1} \atop {x=4}} \right.$

$\displaystyle x^2-3x+2=12 \Rightarrow x^2-3x-10=0 \Rightarrow x^2+2x-5x-10=0 \Rightarrow \\ \Rightarrow x(x+2)-5(x+2)=0 \Rightarrow (x+2)(x-5)=0 \Rightarrow \left [ {{x=-2} \atop {x=5}} \right.$