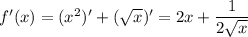Скажите название учебника по фото

N1
а) 4sin³x -8sin²x -sinx +2 =0 ;
4sin²x(sinx-2) -(sinx -2) =0 ;
(sinx -2)(4sin²x -1) = 0 ⇔[ sinx -2 =0 ;4sin²x -1 =0. 
sinx -2 =0⇔sinx =2  ||  > 1 →нет решения.||
4sin²x -1= 0 ⇔4*(1-cos2x)/2 -1 = 0 ⇔cos2x =1/2 ⇒2x =±π/3 +2πk , k∈Z.

ответ: ±π/6 +πk , k∈Z.
---
б)  ;  
(1-cos²x) -2cosx +2 =0  * * *  можно заменить   t =cosx ,  |t| ≤1 * * *
cos²x +2cosx -3  =0 ⇒[cosx = -3(не имеет решения) ; cosx =1.

ответ: 2πk , k∈Z.
-------
N2
а)  ⇔ 7^(5x-1)(7 -1) =6⇔ 7^(5x -1)*6 =6⇔7^(5x -1) =1.
7^(5x -1) =7⁰ ⇒5x-1 =0 ;  x =0,2.
---
б)  ;  
ОДЗ :  { 2x+4 >0 ; 4x -7 >0 ; 4x -7 ≠1. ⇒ x∈(1,75 ;2) U(2 ;∞).

Lq(2x+4) =2Lq(4x-7)⇒Lq(2x+4) =Lq(4x-7)² ;2 x+4 =(4x -7)² ;
16x² -58x +45 =0 ;
D/4 =29² -16*45 =841 -720 =121 =11²
x₁= (29 -11)/16 = 9/8 ∉ОДЗ .
x₂ =(29 +11)/16 = 5/2.

ответ: 2,5.
-------
N3
а)    ;
y ' =( (x² +2x)' (3-4x) - (x² +2x)*(3-4x) ') /(3-4x)² =
( (2x+2)(3 -4x) +4(x² +2x)) /(3-4x)² = -2(2x² -3x-3)/(3-4x)².
---
б)  ;
y ' =((5x+2)⁴) ' =4*(5x+2)³*(5x+2)' =4*(5x+2)³*5=20(5x+2)³ .
-------
N3
а) а)  =(1/6)*x +C.
---
б)  =(-1/3 )интеграл( e^(4-3x)d(4-3x) =(-1/3)e^(4-3x) +C.

1. Здесь в условии опечатка, скорее всего в точке x₀ = -1.

Прямая y=x-2 касается графика функции y=f(x) в точке x₀ = -1, то эта точка является общей для обеих функций, тогда f(-1) = -1-2=-3

ответ: -3.

2. Производная функции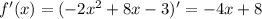

ответ: 16.

3.

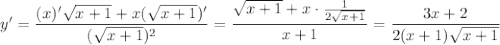
4. Производная функции: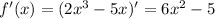

Используем геометрический смысл производной: f'(x₀) = tgα

ответ: 19.

5.

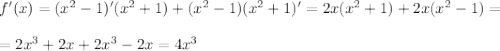
6.

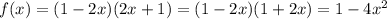
Производная функции: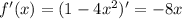 . Производная функции в точке 1, равна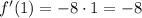

7. Производная функции: f'(x) = 1/2√x, ее значение в точке х=1 равна 1/2. Тогда касательная: y = f'(x0)(x-x0) + f(x0) = 1/2 * (x-1) + 1 = x/2 + 1/2

y(31) = 31/2 + 1/2 = 32/2 = 16

ответ: 16.

8.