Первая скобка это сумма квадратов натуральных чисел и для него имеет место известная формула , а вторая скобка это арифметическая прогрессия с первым членом 1 и разностью d = 1:
Для n = 2019 мы можем подсчитать нашу сумму, т.е.
ответ: 2747468660.
Первая скобка это сумма квадратов натуральных чисел и для него имеет место известная формула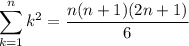 , а вторая скобка это арифметическая прогрессия с первым членом 1 и разностью d = 1:
, а вторая скобка это арифметическая прогрессия с первым членом 1 и разностью d = 1: 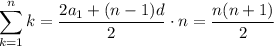
Для n = 2019 мы можем подсчитать нашу сумму, т.е.
ответ: 2747468660.