1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
Переобразуем:
Переносим в общую сторону (левую) и меняем знаки:
Сокрашаем:
ответ:
Старший коэффициент:
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А)
В)
С)
D)
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
Найдите промежутки возрастания и убывания функции, точки экстремума
1) Функция определена на всей области R. Значит она является непрерывной на всей области определения
2) Найдем производную данной функции
Для того, чтобы найти точки экстремума данной функции нужно найти в каких точках производная равна нулю
разделим на 3
Значит точки экстремума х=1 и х=-3
3) Чтобы определить какая из данных точек является точкой максимума, а какая точкой минимума необходимо рассмотреть значение производной на полученных интервалах
___+-+
-3 1
Если производная на промежутке принимает положительное значение то функция на данном промежутке возрастает, если отрицательное- то функция убывает
1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
Переобразуем:
Переносим в общую сторону (левую) и меняем знаки:
Сокрашаем:
ответ: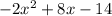
Старший коэффициент: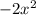
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А)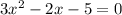
В)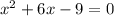
С)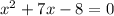
D)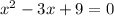
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
A)
2. б) Составьте приведенное квадратное уравнение, имеющие корни х1= 8, х2 = –2.
По теореме Виета:
ответ: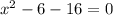
3. Дано квадратное уравнение 2х^2 - 16х + с = 0.
а) Определите, при каких значениях параметра с уравнение имеет два одинаковых корня.
Если дискриминант (D) квадратного уравнения равен 0, то уравнение имеет 1 корень, или говорят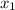 и
и 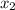 совпадают.
совпадают.
Если p = 0, то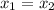
ответ: c = 32
3. б) Найдите эти корни уравнения
ответ: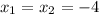
Дальше не знаю как решать(-∞;3) ∪ (
Объяснение:
Найдите промежутки возрастания и убывания функции, точки экстремума
1) Функция определена на всей области R. Значит она является непрерывной на всей области определения
2) Найдем производную данной функции
Для того, чтобы найти точки экстремума данной функции нужно найти в каких точках производная равна нулю
разделим на 3
Значит точки экстремума х=1 и х=-3
3) Чтобы определить какая из данных точек является точкой максимума, а какая точкой минимума необходимо рассмотреть значение производной на полученных интервалах
___+-+
-3 1
Если производная на промежутке принимает положительное значение то функция на данном промежутке возрастает, если отрицательное- то функция убывает
Значит на промежутке (-∞;3) ∪ (