Сколько девяток (цифр) среди чисел от 100 до 700? (решить с формулы)

Показать ответ

Ответ:

123456uiop

13.05.2022 12:55

1) Скорость пасс. поезда равна 465/10,5=4650/105=310/7 км/час.

Скорость тов. поезда равна 465/12=155/4=38,75 км/час .

Пусть до встречи пасс. поезд х км, тогда товарный - (465-х) км.

Время, которое ехал до встречи пасс. поезд, и время, которое до встречи ехал тов. поезд одинаково и равно

$\dfrac{x}{310/7}=\dfrac{465-x}{155/4}\ \ \ ,\ \ \ \dfrac{7x}{310}=\dfrac{4(465-x)}{155} \ \ ,\ \ \ \dfrac{7x}{2}=4(465-x)\ \ ,\\\\\\7x=3720-8x\ \ ,\ \ \ 15x=3720\ \ ,\ \ x=248\ \ ,\ \ \ (465-x)=217$

ответ: пасс. поезд проехал 248 км, а тов. поезд проехал 217 км .

2) Скорость 1 спортсмена равна 100/12 м/с , а второго - 100/13 м/с .

Пусть до встречи 1 спортсмен пробежал х м, тогда 2 спортсмен пробежит (200-х) м .

Время, которое спортсмены бежали до встречи одинаково, поэтому

$\dfrac{x}{100/12}=\dfrac{200-x}{100/13}\ \ ,\ \ \ \dfrac{12x}{100}=\dfrac{13(200-x)}{100}\ \ ,\ \ \ 12x=2600-13x\ \ ,\\\\\\25x=2600\ \ ,\ \ \ x=\dfrac{2600}{25}\ \ ,\ \ x=104 \ \ ,\ \ (200-x)=96$

ответ: 1 спортсмен пробежал 104 м , а 2 спортсмен пробежал 96 м .

0,0(0 оценок)

Ответ:

данил1780

08.04.2022 01:30

Обозначим х -длину одной стороны, у- длину второй стороны. При это х и у > или равны 0

На основании этого составим систему неравенств:

$\left \{ {{x+y14} \atop {x<9}} \right.$

Теперь решим, графически (см. вложение)

Первое уравение рассмотрим как равенство, получим: х+у=14, т.е у=14-х.

Там где на рисунке есть штриховка и синяя и зеленая и лежат наши решения. Значит чтобы найти пределы в которых может изменяться y, нужно найти точку пересечения прямых у=14-х и х=9. Это делается просто в 1 уравение подставляем х=9 и получаем, у=5.

Значит получаем следующее решение (поскольку у нас стороны положительные, то мы рассматриваем только положительную четверть координат).

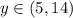
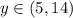И значит решение будет: $y \in (5,14)$