Сколько слов можно составить из слова ЧИСЛО таких, чтобы все гласные буквы стояли рядом?

Показать ответ

Ответ:

egorovnanastya0

03.12.2021 05:01

В решении.

Объяснение:

называется "выделение полного квадрата).

1) х² + 8х - 1 = 0

х² + 8х + 4² - 4² - 1 = 0

(х + 4)² - 17 = 0

(х + 4)² = 17

х + 4 = ±√17

х = ±√17 - 4;

2) 2х² - 5х - 7 = 0/2

↓

х² - 2,5х - 3,5 = 0

х² - 2,5х + 1,25² - 1,25² - 3,5 = 0

(х - 1,25)² - 5,0625 = 0

(х - 1,25)² = 5,0625

х - 1,25 = ±√5,0625

х - 1,25 = ±2,25

х = -2,25 + 1,25

х₁ = -1;

х = 2,25 + 1,25

х₂ = 3,5;

3) 4х² - 16х - 1 = 0/4

↓

х² - 4х - 0,25 = 0

х² - 4х + 2² - 2² - 0,25 = 0

(х - 2)² - 4,25 = 0

(х - 2)² = 4,25

х - 2 = ±√4,25

х - 2 = ±√(0,25*17)

х - 2 = ±0,5√17

х = ±0,5√17 + 2;

4) 5х²/4 - 3х/7 - 3 = 0/5/4

х² - 12х/35 + (6/35)² - (6/35)² - 2,4 = 0

(х - 6/35)² - 2904/1225 = 0

(х - 6/35)² = 2904/1225

х - 6/35 = ±√(2904/1225)

х - 6/35 = ±√((16*186)/1225)

х - 6/35 = (±4√186)/35

х = (±4√186)/35 + 6/35.

Проверка путём подстановки вычисленных значений х в уравнения показала, что данные решения удовлетворяют данным уравнениям.

0,0(0 оценок)

Ответ:

danilkarev201

17.02.2020 14:18

Образы базисных векторов: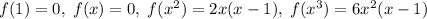 $f(1) = 0,\; f(x) = 0,\; f(x^2) = 2x(x-1),\;f(x^3) = 6x^2(x-1)$ . Разложим образы по базису: 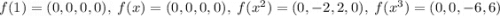$f(1) = (0,0,0,0),\; f(x) = (0,0,0,0),\;f(x^2) = (0,-2,2,0),\;f(x^3) = (0,0,-6,6)$ , потому матрица оператора 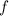будет иметь вид $A=\left(\begin{array}{cccc}0&0&0&0\\0&0&-2&0\\0&0&2&-6\\0&0&0&6\end{array}\right)$ .

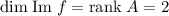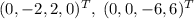(Основа? Понимаю под этим здесь базис, учитывая перевод). Тогда $\mathrm{dim}\;\mathrm{Im} \;f = \mathrm{rank} \;A = 2$ , подойдут, например, векторы $(0,-2,2,0)^{T},\; (0,0,-6,6)^T$ .

$A-\lambda E =\left(\begin{array}{cccc}-\lambda&0&0&0\\0&-\lambda&-2&0\\0&0&2-\lambda&-6\\0&0&0&6-\lambda\end{array}\right) \Rightarrow \chi(\lambda) = \lambda^2(2-\lambda)(6-\lambda)$ , значит, собственные значения -- 0,2,6 .

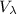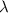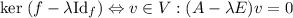Собственное подпространство $V_{\lambda}$ , отвечающее собственному значению $\lambda$ есть в точности $\mathrm{ker}\;(f-\lambda \mathrm{Id}_{f}) \Leftrightarrow v\in V: (A-\lambda E)v = 0$ .

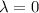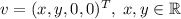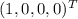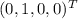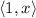Для $\lambda=0$ : $v = (x,y,0,0)^T,\;x,y\in \mathbb{R}$ . Базис можно выбрать, например, такой: $(1,0,0,0)^{T}$ и (0,1,0,0)^T , то есть $\langle 1,x\rangle$ .

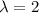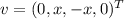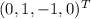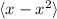Для $\lambda=2$ : v=(0,x,-x,0)^T . Базис: (0,1,-1,0)^T , то есть $\langle x-x^2\rangle$ .

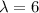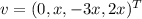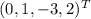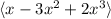Для $\lambda=6$ : v = (0,x,-3x,2x)^T . Базис: (0,1,-3,2)^T , то есть $\langle x-3x^2+2x^3 \rangle$ .

Не слышал понятия простого эндоморфизма, так что предположу, что под этим понимается простой элемент в кольце эндоморфизмов. Ну а тогда идея такая: представить матрицу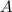 в виде произведения двух матриц, ранг которых выше 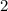(ну а тут только 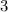) подойдет. Тогда матрица 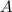не может делить никакую из них. Здесь надо заметить, что наша матрица диагонализуема (алгебраические кратности совпадают с геометрическими), ее можно привести к виду $\left(\begin{array}{cccc}0&0&0&0\\0&0&0&0\\0&0&2&0\\0&0&0&6\end{array}\right)$ . 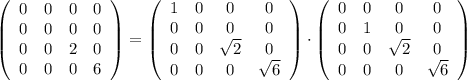Тогда $\left(\begin{array}{cccc}0&0&0&0\\0&0&0&0\\0&0&2&0\\0&0&0&6\end{array}\right) = \left(\begin{array}{cccc}1&0&0&0\\0&0&0&0\\0&0&\sqrt{2}&0\\0&0&0&\sqrt{6}\end{array}\right)\cdot \left(\begin{array}{cccc}0&0&0&0\\0&1&0&0\\0&0&\sqrt{2}&0\\0&0&0&\sqrt{6}\end{array}\right)$ , а ранги сомножителей . Поэтому не является простым.

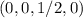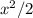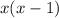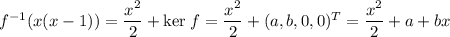После применения оператора получили новый базис (можно было изначально выбрать базис из собственных векторов и тогда бы получили диагональную матрицу из предыдущего пункта). Многочлен x(x-1) в этом (из первого пункта) базисе имеет компоненты (0,0,1/2,0) . Легко видеть, что элемент x^2/2 отображается именно в x(x-1) . Но тогда $f^{-1}(x(x-1)) = \dfrac{x^2}{2}+\mathrm{ker}\;f = \dfrac{x^2}{2}+(a,b,0,0)^T = \dfrac{x^2}{2}+a+bx$ .