На первое место можно разместить любую из пяти цифр, пять На второе место можно разместить любую из четырех цифр, четыре На третье место любую из оставшихся трех цифр, три На все три места результаты выбора умножаем.
5·4·3=60
а) кратны трем те числа, у которых сумма цифр кратна трем
Например, используя цифры 1; 2; 3, сумма цифр которых 1+2=3=6 кратна 3 можно составит шесть чисел, кратных 3:
123; 132;321;312;231;213
Возможностей 4:
1+2+3=6 кратно 3
2+3+4= 9 кратно 3
3+4+5=12 кратно 3
1+3+5=9 кратно 3
В каждой возможности 6 чисел. Всего 24 числа.
б) Кратны четырем те трехзначные числа, у которых две последние цифры кратны 4. Возможны варианты:
*12
*24
*32
*52
На первое место можно разместить любую из оставшихся трех цифр, тремя Всего 3·4=12 чисел
в) кратных 5:
12:
на последнем месте обязательно располагается цифра 5 ( числа кратные 5 оканчиваются на 5 или на 0, 0 у нас нет). На первое место можно выбрать любую из четырех оставшихся цифр - четыре на второе место любую из оставшихся трех - три Всего Подробнее - на -
Вначале заметим, что первообразная скорости равна пройденному пути, откуда имеем следующее:
Для того, чтобы найти путь, пройденной точкой за четвертую секунду, найдем путь, который точка за четыре секунды и за три секунды, а затем из первого вычтем второе.
Считаем разность:
ответ: точка метра за четвертую секунду.
2).
Для нахождения площади этой фигуры можно, во-первых, воспользоваться формулой Ньютона-Лейбница для вычисления интегралов:
В нашем случае (если приравнять и ) .
(как решение уравнения )
(как решение уравнения )
Найдем сам интеграл:
Можно было пойти по-другому: изобразить все на координатной плоскости (смотрите вложенный файл) и по формуле площади прямоугольного треугольника найти площадь :
Всего 60 трехзначных чисел
На первое место можно разместить любую из пяти цифр, пять На второе место можно разместить любую из четырех цифр, четыре На третье место любую из оставшихся трех цифр, три На все три места результаты выбора умножаем.
5·4·3=60
а) кратны трем те числа, у которых сумма цифр кратна трем
Например, используя цифры 1; 2; 3, сумма цифр которых 1+2=3=6 кратна 3 можно составит шесть чисел, кратных 3:
123; 132;321;312;231;213
Возможностей 4:
1+2+3=6 кратно 3
2+3+4= 9 кратно 3
3+4+5=12 кратно 3
1+3+5=9 кратно 3
В каждой возможности 6 чисел. Всего 24 числа.
б) Кратны четырем те трехзначные числа, у которых две последние цифры кратны 4. Возможны варианты:
*12
*24
*32
*52
На первое место можно разместить любую из оставшихся трех цифр, тремя Всего 3·4=12 чисел
в) кратных 5:
12:
на последнем месте обязательно располагается цифра 5 ( числа кратные 5 оканчиваются на 5 или на 0, 0 у нас нет). На первое место можно выбрать любую из четырех оставшихся цифр - четыре на второе место любую из оставшихся трех - три Всего Подробнее - на -
Вначале заметим, что первообразная скорости равна пройденному пути, откуда имеем следующее:
Для того, чтобы найти путь, пройденной точкой за четвертую секунду, найдем путь, который точка за четыре секунды и за три секунды, а затем из первого вычтем второе.
Считаем разность:
ответ: точка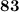 метра за четвертую секунду.
метра за четвертую секунду.
2).Для нахождения площади этой фигуры можно, во-первых, воспользоваться формулой Ньютона-Лейбница для вычисления интегралов:
В нашем случае (если приравнять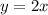 и
и 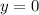 )
) 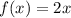 .
.
Найдем сам интеграл:
Можно было пойти по-другому: изобразить все на координатной плоскости (смотрите вложенный файл) и по формуле площади прямоугольного треугольника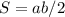 найти площадь
найти площадь 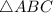 :
:
В обоих случаях получился одинаковый ответ!
ответ: площадь фигуры равна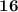 .
.