Ну тут все просто рассмотри каждые суммы по 2 слогаемых, 1-2=-1, 3-4=-1, 5-6=-1. и так далее, т.е. каждый раз мы складываем -1, теперь нужно понять сколько раз мы сложили, очевидно мы складываем пары, а чисел у нас 2020, значит пар у нас 2020/2=1010, умножаем 1010 на -1, получаем ответ.
Второй : сгруппируем слогаемые так, чтобы мы складывали 1+3+5+7, т.е. сумма всех нечетных до 2019, а в оставшейся группе вынесем минус, тогда получится сумма всех четных до 2020. И нужно из суммы всех нечетных вычесть сумму всех нечетных, но вопрос как эти суммы посчитать? ответ - воспользуемся формулой арифмитической прогрессии. Арифм. прог - последовательность чисел, которые отличаются друг от друга на одно и то же число, называемое разностью.
Тогда сумма первых эн членов арифмитической прогрессии равна
удвоенный первый член+ разность прогрессии умножить на кол-во слогаемых минус 1 ,разделить это пополам и умножить на кол-во пар.
Sn=
1-ые члены известны для каждой группы, это единица и двойка. разности тоже одинаковы, и равны двум(т.к. 3-1=2 и 4-2=2)
А вот сколько слогаемых?. Четных и нечетных чисел равное количество от 2020, значит четных 1010 и нечетных столько же
Тогда Сумма четных 2*1+2(1010-1)*1010/2=(1+1009)*1010=1020100
Решение: Сперва определим ОДЗ неравенства. Очевидно, что значение x не должно совпадать со значением 2. Поскольку, знаменатель - это неотрицательное число, то числитель тоже не должен быть отрицательным. Решается методом интервалов. В силу того, что сама дробь должна быть больше 0, то числитель тоже должен быть больше 0 (про знаменатель уже сказали). Как решать неравенство методом интервалов? На вашем примере, думаю, будет все ясно. Находим нули функций (иными словами, находим те значения x, так, чтобы функция была равна 0 и соблюдалось ОДЗ). Это: x=-2;3;4. Отмечаем значения на числовом луче. Определяем знакопостоянство: если x<-2, то числитель отрицателен (отмечаем на луче). При всех остальных значениях числитель - положительный (за исключением x=2, потому что при этом значении знаменатель обращается в нуль, а мы знаем,что на 0 делить нельзя). Получили интервал: отрицательный: И положительный: (рис. 2) Далее, снова отрицательный: И положительный: Но, в условии сказано: найти кол-во целых отрицательных чисел, удовлетворяющих неравенству. Опять же, обращаясь к нашему промежутку чисел, находим, что их только 2: -2 и -1. Однако, -2 обращает дробь в 0, поэтому, число только одно. ответ: -1
-1010
Объяснение:
Ну тут все просто рассмотри каждые суммы по 2 слогаемых, 1-2=-1, 3-4=-1, 5-6=-1. и так далее, т.е. каждый раз мы складываем -1, теперь нужно понять сколько раз мы сложили, очевидно мы складываем пары, а чисел у нас 2020, значит пар у нас 2020/2=1010, умножаем 1010 на -1, получаем ответ.
Второй : сгруппируем слогаемые так, чтобы мы складывали 1+3+5+7, т.е. сумма всех нечетных до 2019, а в оставшейся группе вынесем минус, тогда получится сумма всех четных до 2020. И нужно из суммы всех нечетных вычесть сумму всех нечетных, но вопрос как эти суммы посчитать? ответ - воспользуемся формулой арифмитической прогрессии. Арифм. прог - последовательность чисел, которые отличаются друг от друга на одно и то же число, называемое разностью.
Тогда сумма первых эн членов арифмитической прогрессии равна
удвоенный первый член+ разность прогрессии умножить на кол-во слогаемых минус 1 ,разделить это пополам и умножить на кол-во пар.
Sn=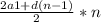
1-ые члены известны для каждой группы, это единица и двойка. разности тоже одинаковы, и равны двум(т.к. 3-1=2 и 4-2=2)
А вот сколько слогаемых?. Четных и нечетных чисел равное количество от 2020, значит четных 1010 и нечетных столько же
Тогда Сумма четных 2*1+2(1010-1)*1010/2=(1+1009)*1010=1020100
Сумма нечетных 4+2(1010-1)*1010/2=(2+1009)*1010=1021110
Вычитаем из первой суммы вторую и получаем -1010
Сперва определим ОДЗ неравенства. Очевидно, что значение x не должно совпадать со значением 2.
Поскольку, знаменатель - это неотрицательное число, то числитель тоже не должен быть отрицательным.
Решается методом интервалов. В силу того, что сама дробь должна быть больше 0, то числитель тоже должен быть больше 0 (про знаменатель уже сказали). Как решать неравенство методом интервалов? На вашем примере, думаю, будет все ясно.
Находим нули функций (иными словами, находим те значения x, так, чтобы функция была равна 0 и соблюдалось ОДЗ). Это: x=-2;3;4. Отмечаем значения на числовом луче. Определяем знакопостоянство: если x<-2, то числитель отрицателен (отмечаем на луче). При всех остальных значениях числитель - положительный (за исключением x=2, потому что при этом значении знаменатель обращается в нуль, а мы знаем,что на 0 делить нельзя). Получили интервал: отрицательный:
И положительный:
Далее, снова отрицательный:
И положительный:
Но, в условии сказано: найти кол-во целых отрицательных чисел, удовлетворяющих неравенству. Опять же, обращаясь к нашему промежутку чисел, находим, что их только 2: -2 и -1. Однако, -2 обращает дробь в 0, поэтому, число только одно.
ответ: -1