1)
ответ: 5
ответ : x принадлежит R
2) ответ: нет решений, т.к. графики не пересекаются
3) Составим таблицу:
1 раствор 2 раствор смесь
концентрация 8 % 16% 11%
масса х мл у мл 400 мл
масса соли х*8/100 у*16/100 400*11/100
Тогда получим два уравнения
х+у=400
0,08х+0,16у=44
Решим полученную систему:
Вычтем из второго уравнения первое:
8x+16y-8x-8y=4400-3200
8y=1200
y=150 мл
Тогда х= 400-150=250 мл
ответ: Первого раствора 250 мл, второго 150 мл
— квадратичная функция, график которой — парабола с ветвями, направленными вверх.
Нули функции:
Согласно теореме Виета, имеем:
По условию или .
Следовательно, подставляя значения и , найдем параметр :
Таким образом, , то есть
Найдем координаты точки вершины параболы:
Значит, — точка вершины параболы.
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
Следовательно, и — точки пересечения функции с осью абсцисс.
б) С осью ординат:
Следовательно, — точка пересечения с осью ординат.
Согласно свойству симметрии параболы, — точка графика.
Изобразим график данной функции (см. вложение).
По условию
Таким образом,
1)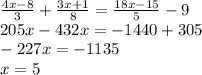
ответ: 5
ответ : x принадлежит R
2) ответ: нет решений, т.к. графики не пересекаются
3) Составим таблицу:
1 раствор 2 раствор смесь
концентрация 8 % 16% 11%
масса х мл у мл 400 мл
масса соли х*8/100 у*16/100 400*11/100
Тогда получим два уравнения
х+у=400
0,08х+0,16у=44
Решим полученную систему:
Вычтем из второго уравнения первое:
8x+16y-8x-8y=4400-3200
8y=1200
y=150 мл
Тогда х= 400-150=250 мл
ответ: Первого раствора 250 мл, второго 150 мл
Нули функции:
Согласно теореме Виета, имеем:
По условию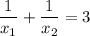 или
или 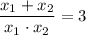 .
.
Следовательно, подставляя значения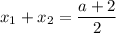 и
и 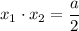 , найдем параметр
, найдем параметр  :
:
Таким образом,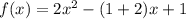 , то есть
, то есть 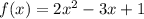
Найдем координаты точки вершины параболы:
Значит,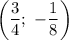 — точка вершины параболы.
— точка вершины параболы.
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
Следовательно,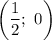 и
и 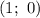 — точки пересечения функции с осью абсцисс.
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
Следовательно,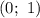 — точка пересечения с осью ординат.
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы,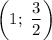 — точка графика.
— точка графика.
Изобразим график данной функции (см. вложение).
Нули функции:
Согласно теореме Виета, имеем:
По условию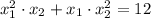
Следовательно, подставляя значения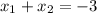 и
и 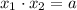 , найдем параметр
, найдем параметр  :
:
Таким образом,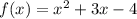
Найдем координаты точки вершины параболы:
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
Следовательно,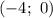 и
и 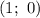 — точки пересечения функции с осью абсцисс.
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
Следовательно,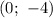 — точка пересечения с осью ординат.
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы,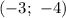 — точка графика.
— точка графика.
Изобразим график данной функции (см. вложение).