Используем геометрическое определение вероятности события A — "встреча с другом состоится".Если площадь S(X) фигуры X разделить на площадь S(A) фигуры A , которая целиком содержит фигуру X, то получится вероятность того, что точка, случайно выбранная из фигуры X, окажется в фигуре A. Обозначим за x и y время прихода, 0≤x,y≤60 (минут), так как время ожидания с 13.00 до 14.00 равно 60 мин. В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата OABC. Друзья встретятся, если между моментами их прихода пройдет не более 6 минут, то есть y-x<6 , y<x+6 (y>x) и x-y<6 , y>x-6 (y<x). Этим неравенствам удовлетворяют точки, лежащие в области Х. Для построения области Х надо построить прямые у=х+6 и у=х-6.Затем рассмотреть точки, лежащие ниже прямой у=х+6 и выше прямой у=х-6. Кроме этого точки должны находиться в квадрате ОАВС. Площадь области Х можно найти, вычтя из площади квадрата ОАВС площадь двух прямоугольных треугольников со сторонами (60-6)=54: S(X)=S(OABC)-2*S(Δ)=60²-2*1/2*54*54=3600-2916=684.
Обозначим за x и y время прихода, 0≤x,y≤60 (минут), так как время ожидания с 13.00 до 14.00 равно 60 мин. В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата OABC. Друзья встретятся, если между моментами их прихода пройдет не более 6 минут, то есть
y-x<6 , y<x+6 (y>x) и
x-y<6 , y>x-6 (y<x).
Этим неравенствам удовлетворяют точки, лежащие в области Х.
Для построения области Х надо построить прямые у=х+6 и у=х-6.Затем рассмотреть точки, лежащие ниже прямой у=х+6 и выше прямой у=х-6.
Кроме этого точки должны находиться в квадрате ОАВС.
Площадь области Х можно найти, вычтя из площади квадрата ОАВС площадь двух прямоугольных треугольников со сторонами (60-6)=54:
S(X)=S(OABC)-2*S(Δ)=60²-2*1/2*54*54=3600-2916=684.
Решим задачу, используя геометрическую вероятность.
Пусть![x,y\in[0;\ 60]](/tpl/images/1102/9312/1412e.png) - минута прибытия первого и второго.
- минута прибытия первого и второго.
Встреча произойдет, если выполнится условие: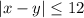 . Перепишем условие в виде:
. Перепишем условие в виде:
Изобразим графически это условие - получим шестиугольник. Его площадь соответствует благоприятным исходам.
Общая площадь - площадь квадрата - соответствует всем возможным исходам.
Отношение площади шестиугольника к площади квадрата и даст искомую вероятность.
Площадь шестиугольника найдем как разность между площадью квадрата и площадью двух незакрашенных треугольников.
ответ: 0.36