Заметим, что сумма цифр у числа будет иметь такой же остаток по модулю 9, что и само число, так как пусть число имеет вид заметим, что число вида 10^n-1 делится на 9, так как оно будет состоять из одних девяток, значит число вида сравнимо с по модулю 9. Значит все число сравнимо с суммой цифрой по модулю 9. Так как 209! делится на 9 (содержит множитель 9), то сумма цифр будет делится на 9 ⇒ сумма суммы цифр делится на 9 и. т.д. Таким образом, однозначное число будет делится на 9, значит оно равно 0 или 9, но равно 0 оно быть не может, так как сумма цифр у натурального числа ненулевая, так как содержит хотя бы 1 не 0. Значит она равна 9
1) (2a + 5b) + (8a - 11b) + (9b - 5a) = 2a + 5b + 8a - 11b + 9b - 5a =
= (2a + 8a - 5a) + (5b - 11b + 9b) = 5a + 3b
2) (3х + 10у) – (6х + 3у) + (6у – 8х) = 3х + 10у – 6х - 3у + 6у – 8х =
= (3x - 6x - 8x) + (10y- 3y + 6y) = - 11x + 13y
3) (8с² + 3с) + (- 7с² – 11с + 3) – (- 3с² – 4) = 8с² + 3с - 7с² – 11с + 3 + 3с² + 4 =
= (8c² - 7c² + 3c²) + (3c - 11c) + (3 + 4) = 4c² - 8c + 7
4) (2р² + 3рс + 8с²) – (6р² – рс – 8с²) = 2р² + 3рс + 8с² – 6р² + рс + 8с²=
= (2p² - 6p²) + (8c² + 8c²) + (3pc + pc) = - 4p² + 16c² + 4pc
5) 10х² – (7ах – 5х² + 8а²) + (6ах – 4а²) = 10х² – 7ах + 5х² - 8а² + 6ах – 4а²=
= (10x² + 5x²) + (- 7ax + 6ax) + (- 8a² - 4a²) = 15x² - ax - 12a²
9
Объяснение:
Заметим, что сумма цифр у числа будет иметь такой же остаток по модулю 9, что и само число, так как пусть число имеет вид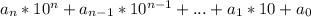
заметим, что число вида 10^n-1 делится на 9, так как оно будет состоять из одних девяток, значит число вида 
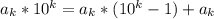сравнимо с 
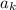по модулю 9. Значит все число сравнимо с суммой цифрой по модулю 9. Так как 209! делится на 9 (содержит множитель 9), то сумма цифр будет делится на 9 ⇒ сумма суммы цифр делится на 9 и. т.д. Таким образом, однозначное число будет делится на 9, значит оно равно 0 или 9, но равно 0 оно быть не может, так как сумма цифр у натурального числа ненулевая, так как содержит хотя бы 1 не 0. Значит она равна 9