допустим что стороны прямоугольника A и B, и площадь S. Тогда S=A*B (площадь равно произведению сторон). Далее сказано, что одна сторона больше другой на 11 см. доопустим A=B+11. следовательно можно составить уравнение: S=(B+11)*B. Далее у нас сказано, что площадь равна 60 см(в квадрате). Следовательно составляем квадратное уравнение:
Далее решаем как обычное квадратное уравнение. В итоге получим что . Меньше нуля быть не может, поэтому B=4. А т.к. А=B+11, то А=4+11=15.
допустим что стороны прямоугольника A и B, и площадь S. Тогда S=A*B (площадь равно произведению сторон). Далее сказано, что одна сторона больше другой на 11 см. доопустим A=B+11. следовательно можно составить уравнение: S=(B+11)*B.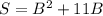 Далее у нас сказано, что площадь равна 60 см(в квадрате). Следовательно составляем квадратное уравнение:
Далее у нас сказано, что площадь равна 60 см(в квадрате). Следовательно составляем квадратное уравнение: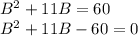
Далее решаем как обычное квадратное уравнение. В итоге получим что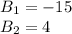 . Меньше нуля быть не может, поэтому B=4. А т.к. А=B+11, то А=4+11=15.
. Меньше нуля быть не может, поэтому B=4. А т.к. А=B+11, то А=4+11=15.
А=15
и B=4.
Периметр будет равен (A+B)*2=(15+4)*2=19*2=38см.
№1
1) ab-ac+yb-yc=a(b-c)+y(b-c)=(a+y)(b-c)
2)3x+3y-bx-by=3(x+y)-b(x+y)=(3-b)(x+y)
3) 4a-ab-4+b=a(4-b)-1(4-b)=(a-1)(4-b)
4) а^7+а^3 -4a^4-4=a^3(a^4+1)-4(a^4+1)=(a^3-4)(a^4+1)
5) 6ху-3x+2y-1=3x(2y-1)+1(2y-1)=(3x+1)(2y-1)
6) 4х^4-5х^3y-8х+10y=x^3(4-5y)-2(4-5y)=(x^3-2)(4-5y)
№2
1) 8a^2-8aв-5а+5в, если а = 8 , в = 4
8a^2-8aв-5а+5в=8a(a-в)-5(а-в)=(8а-5)(а-в)
(8*8-5)(8-4)=59*4=236 ответ: 236
2) 10х^3+х^2+10х+1, если х = 0,3
10х^3+х^2+10х+1=x^2(10x+1)+1(10x+1)=(x^2+1)(10x+1)
(0,3^2+1)(10*0,3+1)=1,09*4=4,36 ответ: 4,36