Сьогодні 1)x=3;
2) |x-31=2;
3)|*-41=0;
4) (x+3)=-4;
5) |x|+1=7;
6)|*|-2=-3;
7) 3|*|-1=0;
8) 2x +3=0;
9) (3x +21-4=0; o
10) |2x - 11+7=8
Дз алг
11:24
*,
49. Розв'яжіть рівняння:
5r-4_16x+1
2)
4y + 33 17+у.
2
3
50.1 Знайдіть корінь рівняння:
Зm +5 бm +1
1)
5х + 3
+1;
4
3
8
51. Чому дорівнює корінь рівняння:
2х5х
7.
3)
Зr
3
6 36
10
52. Розв'яжіть рівняння:
7x 5x 4
15
1)
6 18 27
7 4 14
4 x2
1) - 23;
12
Дз алг
Переведем все значения в градусы, чтобы было привычнее.
π=180°
/ - так обозначается черта дроби.
переведу число -0,5 в дробь, тоже для удобства = -1/2
sin(180°/4-a) если cos a = -1/2 ; 180°/2<a<180°
sin(45°-a) если cos a= -1/2;
90<a<180° по условию угол находится во второй четверти. Синус в этой четверти принимает только положительные значения.
Как найти sin a? Вспомним основное тригонометрическое тождество:
cos²a+sin²a=1, отсюда выразим наш синус:
sin²a= 1-cos²a.
Чтобы найти sin a, возведем в корень 1-cos²a
Получаем: sin a = √1-cos²a.
Подставляем известное нам выражение cos a, которое мы не забываем возвести в квадрат.
sin a = √1-(-1/4) = √1+1/4 = √5/4 = √5/2
sin(45°-a)=sin45°cosa-cos45°sina= √2/2*(-1/2)-√2/2*√5/2=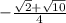 Помним, что синус во второй четверти положительный.
Помним, что синус во второй четверти положительный.
Получаем ответ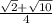
Характеристическое свойство арифметической прогрессии: каждый член арифметической прогрессии, начиная со второго, равен полусумме предыдущего и последующего члена.
Значит, нужно доказать, что:
Выполняем преобразования:
Выражаем b и с через а и d:
Слева и справа записаны одинаковые выражения. Значит, заданные числа удовлетворяют характеристическому свойству и являются последовательными членами арифметической прогрессии