Сократи дробь x+6
x2+26x+120

a) Рассмотри график функции y=x^2+3x+3
Найдем точки пересечения с осью Ох, решив уравнение x^2+3x+3=0
D = 9 - 4*3= - 3
Т.к. D = -3 < 0 ,
Следовательно, график y=x^2+3x+3 не пересекает ось Ох 
Т.к. коэффициент при x^2 = 1>0 , то ветви графика (ветви параболы) направлены вверх, следовательно график полностью распологается выше оси Ох и соответственно при любых значениях переменной х, значение квадратного трехчлена x^2+3x+3-положительно

б) Рассуждения аналогичны предыдущему примеру
Вычислим дискриминант для уравнения 4x-4x^2-2=0
D = 16 - 4*4*2 = -16
Следовательно, график y=4x-4x^2-2 не пересекает ось Ох 
Т.к. коэффициент при x^2 = -4<0 , то ветви графика (ветви параболы) направлены вниз, следовательно график полностью распологается ниже оси Ох и соответственно при любых значениях переменной х, значение квадратного трехчлена 4x-4x^2-2-отрицательно

Примем за 1 - объем цистерны

Пусть t цис./ч - производительность "медленного" насоса.

Тогда 3t цис./ч - производительность "быстрого" насоса.

(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.

(t+3t)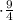 - объем работы системы из двух насосов за 2ч 15мин.

Получим уравнение: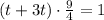

9t = 1

Значит,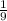 - цис./ч - производительность "медленного" насоса.

Тогда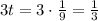 - цис./ч - производительность "быстрого" насоса.

Следовательно,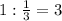 ч - потребуется "быстрому" насосу на заполнение цистерны.

ответ: 3 ч.