Букв у нас 10, 3 буквы А, по 2 буквы М и Т, и по одной Е, И и К. На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10! Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы. Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами. Для М и Т это будет 2! и 2!, для А – 3! С учётом порядка позиции их будет: Тогда вероятность (согласно классическому определению):
Попробуем другой, более простой Перестановки с повторением. Всего у нас Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность:
На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10!
Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы.
Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами.
Для М и Т это будет 2! и 2!, для А – 3!
С учётом порядка позиции их будет:
Тогда вероятность (согласно классическому определению):
Попробуем другой, более простой
Перестановки с повторением.
Всего у нас
Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность:
1. Область определения: На ноль делить нельзя -->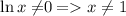
и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
2. Функция общего вида т.к. f(-x)≠±f(x)
3. Точки пересечения с осями:
4. Исследование с 1ой производной:
см. внизу.
5. Исследование со 2ой производной:
см. внизу.
6. Асимптоты:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: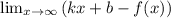
Находим коэффициент k: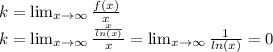
Находим коэффициент b: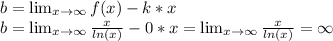
Предел равен ∞, следовательно, наклонные асимптоты функции отсутствуют.
Найдем вертикальные асимптоты. Для этого определим точки разрыва: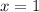
Находим переделы в точке 1: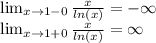
Значит точка разрыва II рода и является вертикальной асимптотой.