Составь математическую модель по словесной: сумма катетов прямоугольного треугольника равна 7 дм , а его гипотенуза равна 5 дм . Определи площадь треугольника.
Выбери подходящую математическую модель, обозначив длину одного катета как a дм , а другого — y дм :
1) скорость лодки по течению 6,5 км/ч
2 )скорость пешехода 5 км/ч, скорость велосипедиста 15 км/ч
Объяснение:
1) x - скорость лодки по течению реки
х - 2 -скорость лодки в море
х - 2 - 2 = х - 4 -скорость лодки против течения
18(х - 4) = 10(х - 2)
18х - 72 = 10х - 20
8х = 52
х = 6,5 (км/ч)
2) х - скорость пешехода
х + 10 - скорость велосипедиста
25x + 250 - 30x = 3x² + 30x
3x² + 35x - 250 = 0
D = 35²+ 4 · 3 · 250 = 4225
√D = 65
x₁ = (-35 - 65) : 6 = - 50/3 - не подходит по физическому смыслу скорости
х₂ = (-35+65) : 6 = 5 (км/ч) - скорость пешехода
х + 10 = 15 (км/ч) - скорость велосипедиста
Пусть АВСD - данная трапеция, AB || CD; AB = AD;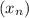
- арифметическая прогрессия.
Пусть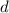
- разность прогрессии, AB = 
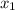По формуле 
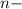ого члена имеем: BC = 
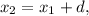CD =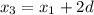 
Периметр трапеции равен: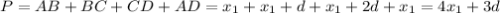
, т.е.
Опустим высоту BK = AD =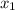
⇒ ABKD - квадрат ⇒ KD = 
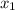⇒ CK = CD - KD = 
=
.
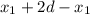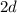В ΔВКС (∠К = 90°) по теореме Пифагора: ВС² = ВК² + СК² =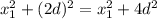
⇒ 
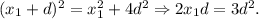
Имеем систему:
Тогда AD = AB = 24 дм, BC = 24 + 16 = 40 дм, CD = 24 + 2 · 16 = 56 дм.
ОТВЕТ: 24 дм; 24 дм; 40 дм; 56 дм.
Доп. вопросы:
1. d = 16
2. Теорема Пифагора
3. Неравенство треугольника: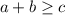
4. Сторона основания (CD).