Пусть точка касания равна . Составим уравнение касательной к графику функции в этой точке.
Уравнение касательной:
Так как касательная проходит через точку , то подставим ее координаты в уравнение:
Проверим получающиеся уравнения касательной. Если :
- прямая параллельна оси абсцисс - противоречие условию
Если :
- корректное уравнение касательной
ответ: 1
Пусть точка касания равна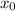 . Составим уравнение касательной к графику функции
. Составим уравнение касательной к графику функции 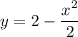 в этой точке.
в этой точке.
Уравнение касательной:
Так как касательная проходит через точку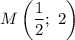 , то подставим ее координаты в уравнение:
, то подставим ее координаты в уравнение:
Проверим получающиеся уравнения касательной. Если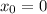 :
:
Если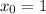 :
:
ответ: 1