(см. объяснение)
Объяснение:
Теория:
Если в формулу вместо , и поставить произвольные числа и выполнить перемножение скобок, то получится многочлен второй степени, который имеет корни и .
Опираясь на теорию выше, составим 3 квадратных уравнения.
Каждое из них имеет корни и .
Тогда возьмем 3 произвольных значения a.
1)
Пусть a=20.
Тогда:
Итого наше уравнение имеет вид:
2)
Пусть a=3.
Тогда уравнение примет вид:
3)
Пусть a=1.
Задание выполнено!
(см. объяснение)
Объяснение:
Теория:
Если в формулу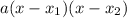 вместо
вместо 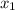 ,
, 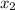 и
и  поставить произвольные числа и выполнить перемножение скобок, то получится многочлен второй степени, который имеет корни
поставить произвольные числа и выполнить перемножение скобок, то получится многочлен второй степени, который имеет корни 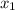 и
и 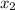 .
.
Опираясь на теорию выше, составим 3 квадратных уравнения.
Каждое из них имеет корни и
и  .
.
Тогда возьмем 3 произвольных значения a.
1)
Пусть a=20.
Тогда:
Итого наше уравнение имеет вид:
2)
Пусть a=3.
Тогда уравнение примет вид:
3)
Пусть a=1.
Тогда:
Задание выполнено!