Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
braskyn
23.08.2020 23:55 •
Алгебра
Составьте уравнение касательной к графику функции y = 2x^3 + 1/3 * x^2 в точке с абсциссой x0 = -3
Показать ответ
Ответ:
майя155
14.10.2020 12:29
ответ:
Объяснение:
0,0
(0 оценок)
Популярные вопросы: Алгебра
ekaterinaf79
12.05.2020 13:26
Вычислите:√5 целых один седьмых×3 целых четыре седьмыхв корне пять относительных умножаем на 3 4/7 всё это в корне 5 1/7 х 3 4/7 как будет скажите мне очень-очень...
klimsamgim923dushez
07.07.2022 12:54
Решите подстановки ситему уравнений...
sashak73
14.07.2020 12:09
Решение примеров 1.(5,6-х) (2х+9)=02.5х/6-3х/12=5/24...
AnTonDPR
19.03.2021 12:34
3.Вкажіть правильну нерівність:А)-6,64:6,71 Б)-0,23-0,34B)-0,01-0,002 Г)5,1 -6,9...
RIGBY19204
14.06.2022 09:42
Бірінші құбыр екіншіге қарағанда 4 л су кем өткізеді. Көлемі 384 л болатын су қоймасын толтыратын екінші құбырға қарағанда бірінші құбыр көлемі 480 л болатын су қоймасын...
rogaoksi
05.10.2022 12:45
Известно что a²+b²=12, c²+d²=3 довести что |ac+bd|= 6 умников, которые рандномно проходятся по клавиатуре не вмешиваться...
buldog228
18.05.2021 03:47
Решите уравнение через димкриминант или через теорему виета в полном объёме с ответом pls...
nagornaykisa
13.11.2020 23:42
Вычисли значения выражения √6-2a если a=1...
vadimkolknev
01.03.2023 12:32
A/12b+27b/a =3 , не пишите неправильные ответы ;)нужно доказать неравенство...
Evgenn4ik
28.04.2020 14:54
Решите графическ уравнение квадратный корень x=4-x\2...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
ответ: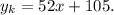
Объяснение: