Общий вид уравнения касательной:
Вычислим производную функции:
Используя геометрический смысл производной
получим
Абсциссы точки касания: x0 = ±2.
Вычислим значение функций в точке х0=±2.
Определим значение производной функции в точке x0=±2
Искомые уравнения касательных:
Общий вид уравнения касательной: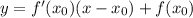
Вычислим производную функции:
Используя геометрический смысл производной
получим
Абсциссы точки касания: x0 = ±2.
Вычислим значение функций в точке х0=±2.
Определим значение производной функции в точке x0=±2
Искомые уравнения касательных: