Посчитаем сначала количество чисел, записываемых цифрами от до , а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
Выпишем числа от до : . Любые вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть: .
Теперь посчитаем количество тех, в которых есть четыре подряд идущих. В этом случае мы можем вычеркивать только из -ех оставшихся чисел. Поскольку четверок подряд идущих , то всего искомых чисел .
Дан прямоугольник, периметр которого равен 8 см. Тогда сумма двух сторон равна 8:2 = 4 см. Обозначим через x одну сторону прямоугольника. Тогда вторая сторона равна: 4–x. Теперь составим функцию площади прямоугольника: y=x·(4–x)=4·x-x². Дифференцируем функцию
Посчитаем сначала количество чисел, записываемых цифрами от до
до 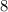 , а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
, а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
Выпишем числа от до
до 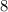 :
: 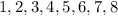 . Любые
. Любые 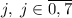 вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть:
вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть: 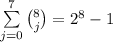 .
.
Теперь посчитаем количество тех, в которых есть четыре подряд идущих. В этом случае мы можем вычеркивать только из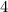 -ех оставшихся чисел. Поскольку четверок подряд идущих
-ех оставшихся чисел. Поскольку четверок подряд идущих 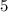 , то всего искомых чисел
, то всего искомых чисел 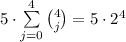 .
.
Итого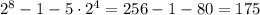 .
.
2 см и 2 см
Объяснение:
Дан прямоугольник, периметр которого равен 8 см. Тогда сумма двух сторон равна 8:2 = 4 см. Обозначим через x одну сторону прямоугольника. Тогда вторая сторона равна: 4–x. Теперь составим функцию площади прямоугольника: y=x·(4–x)=4·x-x². Дифференцируем функцию
y'=(4·x–x²)'=4–2·x.
Находим критические точки функции:
y'=0 ⇔ 4–2·x=0 ⇔ x=2 – критическая точка.
Проверим знаки производной:
при x<2: y'=4–2·x>0 и при x>2: y'=4–2·x<0.
Значит, x=2 точка максимума. Тогда
yмакс=y(2)=4·2–2²=8–4=4 см²,
а стороны x=2 см и 4–2=2 см.